题目内容
如图，△ABC中，AD为∠A的平分线，证明：
=
．
| CD |
| DB |
| AC |
| AB |
考点：正弦定理
专题：证明题
分析：根据正弦定理和角的相等和互补可得．
解答：
证明：在△ABD中，由正弦定理得：
=
，
同理，在△ADC中有，
=
，
由于sin∠ADB=sin∠ADC，∠BAD=∠CAD，
两式相比得：
=
．
| BD |
| sin∠BAD |
| AB |
| sin∠ADB |
同理，在△ADC中有，
| CD |
| sin∠CAD |
| AC |
| sin∠ADC |
由于sin∠ADB=sin∠ADC，∠BAD=∠CAD，
两式相比得：
| CD |
| DB |
| AC |
| AB |
点评：本题主要考查正弦定理的应用，属于基础题．
练习册系列答案
相关题目
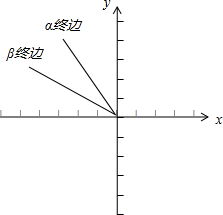已知α是第二象限角，在第二象限内将角α的终边绕原点按逆时针方向旋转，得到第二象限角β的终边，如图所示，利用单位圆中的三角函数线比较下列各组数的大小．