题目内容
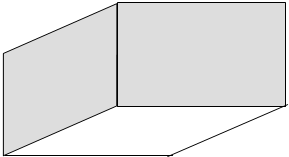 如图,用一块长为2米,宽为1米的矩形木板,在教室的墙角处围出一个直三棱柱的储物角(使木板垂直于地面的两边与墙面贴紧),试问应怎样围才能使储物角的容积最大?并求出这个最大值.
如图,用一块长为2米,宽为1米的矩形木板,在教室的墙角处围出一个直三棱柱的储物角(使木板垂直于地面的两边与墙面贴紧),试问应怎样围才能使储物角的容积最大?并求出这个最大值.考点:棱柱、棱锥、棱台的体积
专题:应用题,空间位置关系与距离
分析:求出以木板的宽为三棱柱的高时,围成的三棱柱的体积是多少,
再求出以木板的长为三棱柱的高时,围成的三棱柱的体积是多少,二者比较得出结论.
再求出以木板的长为三棱柱的高时,围成的三棱柱的体积是多少,二者比较得出结论.
解答:
解:设木板与一面墙的夹角为θ,以木板宽1为三棱柱的高,
则棱柱的底面积是:
S=
•2cosθ•2sinθ=sin2θ≤1,当θ=
时等号成立;
此时棱柱的体积V1=hS=1×1=1;
若以木板的长2为三棱柱的高,
则最大体积为V2=2×
=
,
∴V1>V2,
∴应取底面为等腰三角形,且高为1时,围成的容积最大.
则棱柱的底面积是:
S=
| 1 |
| 2 |
| π |
| 4 |
此时棱柱的体积V1=hS=1×1=1;
若以木板的长2为三棱柱的高,
则最大体积为V2=2×
| 1 |
| 4 |
| 1 |
| 2 |
∴V1>V2,
∴应取底面为等腰三角形,且高为1时,围成的容积最大.
点评:本题考查了三棱柱的体积计算问题,也考查了实际应用问题,解题的关键是设计出两种围成的三棱柱的方案,是中档题.

练习册系列答案
相关题目
已知椭圆过点P(
,-4)和点Q(-
,-3),则此椭圆的标准方程是( )
| 3 |
| 5 |
| 4 |
| 5 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、以上均不正确 |