题目内容
一名箭手进行射箭训练,箭手连续射2支箭,已知射手每只箭射中10环的概率是
,射中9环的概率是
,射中8环的概率是
,假设每次射箭结果互相独立.
(1)求该射手两次射中的总环数为18环的概率;
(2)求该箭手两次射中的总环数为奇数的概率.
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
(1)求该射手两次射中的总环数为18环的概率;
(2)求该箭手两次射中的总环数为奇数的概率.
考点:离散型随机变量的期望与方差
专题:概率与统计
分析:(1)该射手两次射中的总环数为18环的情况有两种:①10环和8环各一次;②两次都是9环.由此能求出该射手两次射中的总环数为18环的概率.
(2)该箭手两次射中的总环数为奇数的情况有两种:①10环和9环各一次;②9环和8环各一次.由此能求出该箭手两次射中的总环数为奇数的概率.
(2)该箭手两次射中的总环数为奇数的情况有两种:①10环和9环各一次;②9环和8环各一次.由此能求出该箭手两次射中的总环数为奇数的概率.
解答:
解:(1)该射手两次射中的总环数为18环的情况有两种:
①10环和8环各一次;②两次都是9环.
∴该射手两次射中的总环数为18环的概率:
p1=
×
+
×
+
×
=
.
(2)该箭手两次射中的总环数为奇数的情况有两种:
①10环和9环各一次;②9环和8环各一次.
∴该箭手两次射中的总环数为奇数的概率:
p2=
×
+
×
+
×
+
×
=
.
①10环和8环各一次;②两次都是9环.
∴该射手两次射中的总环数为18环的概率:
p1=
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 5 |
| 16 |
(2)该箭手两次射中的总环数为奇数的情况有两种:
①10环和9环各一次;②9环和8环各一次.
∴该箭手两次射中的总环数为奇数的概率:
p2=
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 8 |
点评:本题考查概率的求法,解题时要认真审题,注意相互独立事件同时发生的概率计算公式的合理运用,是中档题.

练习册系列答案
相关题目
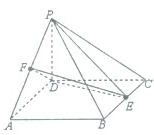 如图,四棱锥P-ABCD的底面ABCD为菱形,PD⊥平面ABCD,PD=AB=2,∠BAD=60°,E、F分别为BC、PA的中点.
如图,四棱锥P-ABCD的底面ABCD为菱形,PD⊥平面ABCD,PD=AB=2,∠BAD=60°,E、F分别为BC、PA的中点.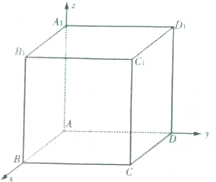 如图所示,以正方体的顶点A为坐标原点,棱AB、AD、AA1所在的直线为x,y,z轴建立空间直角坐标系,且正方体的棱长为2,则该正方体外接球的球心坐标为
如图所示,以正方体的顶点A为坐标原点,棱AB、AD、AA1所在的直线为x,y,z轴建立空间直角坐标系,且正方体的棱长为2,则该正方体外接球的球心坐标为