题目内容

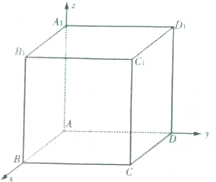如图所示，以正方体的顶点A为坐标原点，棱AB、AD、AA1所在的直线为x，y，z轴建立空间直角坐标系，且正方体的棱长为2，则该正方体外接球的球心坐标为
 
．
考点：空间中的点的坐标
专题：空间位置关系与距离
分析：正方体的体对角线就是外接球的直径，体对角线的中点就是外接球的球心，求出坐标即可．
解答： 解：正方体的体对角线就是外接球的直径，体对角线的中点就是外接球的球心，
即AC1的中点就是球心，球心坐标为：（1，1，1）．
故答案为：（1，1，1）．
点评：本题考查空间中点的坐标的求法，外接球与几何体的关系，判断球心位置是解题的关键．
练习册系列答案
相关题目
某花店每天以每枝10元的价格从农场购进若干支玫瑰花，并开始以每枝20元的价格出售，已知该花店的营业时间为8小时，若前7小时内所购进的玫瑰花没有售完，则花店对没卖出的玫瑰花以每枝5元的价格低价处理完毕（根据经验，1小时内完全能够把玫瑰花低价处理完毕，且处理完毕后，当天不再购进玫瑰花）．该花店统计了100天内玫瑰花在每天的前7小时内的需求量n（单位：枝，n∈N*）（由于某种原因需求量频数表中的部分数据被污损而无法看清），制成如下表格（注：x，y∈N*；视频率为概率）．
前7小时内的需求量n14151617
频数1020xy
（Ⅰ）若花店一天购进16枝玫瑰花，X表示当天的利润（单位：元），求X的分布列及数学期望；
（Ⅱ）若花店每天购进16枝玫瑰花所获得的平均利润比每天购进17枝玫瑰花所获得的平均利润大，求x的取值范围．
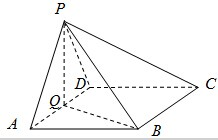如图四棱锥P-ABCD的底面ABCD为菱形，∠BAD=60°，Q为AD的中点．
（1）若PA=PD，求证：平面PQB⊥平面PAD；
（2）若PA=PD=AD，且平面PAD⊥平面ABCD，点M是线段PC的中点，求平面MBQ与平面ABCD所成角的余弦值．
一名箭手进行射箭训练，箭手连续射2支箭，已知射手每只箭射中10环的概率是
1
4
，射中9环的概率是
1
4
，射中8环的概率是
1
2
，假设每次射箭结果互相独立．
（1）求该射手两次射中的总环数为18环的概率；
（2）求该箭手两次射中的总环数为奇数的概率．
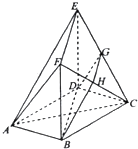如图，在多面体ABCDEF中，底面ABCD是边长为2的正方形，四边形BDEF是矩形，平面BDEF⊥平面ABCD，BF=3，G和H分别是CE，CF的中点．
（1）求证：AC⊥平面BDEF；
（2）求证：平面BDGH∥平面AEF；
（3）求多面体ABCDEF的体积．
某校有3300名学生，其中高一、高二、高三年级学生人数比例为12：10：11，现用分层抽样的方法，随机抽取66名学生参加一项体能测试，则抽取的高二学生人数为
 
．
在△ABC中，a，b，c分别为∠A，∠B，∠C所对的边，且cosA=
4
5
，
sinB
sinA
=
b
2
，则△ABC的面积S的最大值为
 
．
已知定义在R上的函数f（x），满足f（-x）=-f（x），f（x-3）=f（x），当x∈（0，
3
2
）时，f（x）=ln（x2-2x+2），则函数f（x）在区间[-2，2]上的零点个数是
 
．
在极坐标系中，过点（3，
π
3
）且垂直于极轴的直线方程的极坐标方程是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网