题目内容
已知圆M:x2+y2-4x+2y+c=0与y轴交于A,B两点,圆心为M,且∠AMB=90°.
(Ⅰ)求c的值;
(Ⅱ)若圆M与直线x+y-1=0交于E,F两点,且E,F的横坐标xE<yF,动点H到E,F两点的距离的比为λ(λ>0),求点H的轨迹方程,并说明它是什么图形.
(Ⅰ)求c的值;
(Ⅱ)若圆M与直线x+y-1=0交于E,F两点,且E,F的横坐标xE<yF,动点H到E,F两点的距离的比为λ(λ>0),求点H的轨迹方程,并说明它是什么图形.
考点:轨迹方程,直线和圆的方程的应用
专题:综合题,直线与圆
分析:(Ⅰ)利用△AMB为等腰直角三角形,可求c的值;
(Ⅱ)求出E,F的坐标,利用动点H到E,F两点的距离的比为λ(λ>0),可得轨迹方程.
(Ⅱ)求出E,F的坐标,利用动点H到E,F两点的距离的比为λ(λ>0),可得轨迹方程.
解答:
解:(Ⅰ)圆M:x2+y2-4x+2y+c=0可化为(x-2)2+(y+1)2=5-c,
∵∠AMB=90°,
∴△AMB为等腰直角三角形,
∴5-c=8,
∴c=-3;
(Ⅱ)直线x+y-1=0代入x2+y2-4x+2y-3=0,∵xE<yF,∴E(0,1),F(4,-3).
设H(x,y),则
|HE|2=x2+(y-1)2,|HF|2=(x-4)2+(y+3)2,
∵动点H到E,F两点的距离的比为λ(λ>0),
∴(1-λ2)x2+(1-λ2)y2+8λ2x-(2+6λ2)y+1-25λ2=0,
λ=1时,方程为x-y-3=0,轨迹为线段EF的垂直平分线,
λ≠1时,方程表示以(-
,
)为圆心,
为半径的圆.
∵∠AMB=90°,
∴△AMB为等腰直角三角形,
∴5-c=8,
∴c=-3;
(Ⅱ)直线x+y-1=0代入x2+y2-4x+2y-3=0,∵xE<yF,∴E(0,1),F(4,-3).
设H(x,y),则
|HE|2=x2+(y-1)2,|HF|2=(x-4)2+(y+3)2,
∵动点H到E,F两点的距离的比为λ(λ>0),
∴(1-λ2)x2+(1-λ2)y2+8λ2x-(2+6λ2)y+1-25λ2=0,
λ=1时,方程为x-y-3=0,轨迹为线段EF的垂直平分线,
λ≠1时,方程表示以(-
| 4λ2 |
| 1-λ2 |
| 1+3λ2 |
| 1-λ2 |
4
| ||
| |1-λ2| |
点评:本题考查直线与圆的位置关系,考查轨迹方程,考查小时分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
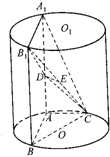 如图,AA1、BB1为圆柱OO1的母线,BC是底面圆O的直径,D、E分别是AA1、CB1的中点,AB=AC.
如图,AA1、BB1为圆柱OO1的母线,BC是底面圆O的直径,D、E分别是AA1、CB1的中点,AB=AC. 为了了解青少年视力情况,某市从高考体检中随机抽取16名学生的视力进行调查,经医生用对数视力表检查得到每个学生的视力状况的茎叶图(以小数点前的一位数字为茎,小数点后的一位数字为叶)如图所示.
为了了解青少年视力情况,某市从高考体检中随机抽取16名学生的视力进行调查,经医生用对数视力表检查得到每个学生的视力状况的茎叶图(以小数点前的一位数字为茎,小数点后的一位数字为叶)如图所示.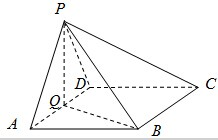 如图四棱锥P-ABCD的底面ABCD为菱形,∠BAD=60°,Q为AD的中点.
如图四棱锥P-ABCD的底面ABCD为菱形,∠BAD=60°,Q为AD的中点.