题目内容
三角形ABC中，过中线AD的中点E作直线分别与边AB和AC交于M、N两点，若
=x
，
=y
，则4x+y的最小值是 ．
| AM |
| AB |
| AN |
| AC |
考点：平面向量的基本定理及其意义
专题：
分析：根据向量的加法及条件，
既可用
，
表示，又可用
，
表示，所以分别表示完之后便得到
=(
-x)
+
和
=
+(
-y)
，这时候，寻找一下
和
的关系，发现这两个向量共线，根据共线向量基本定理便知道存在实数λ，使得
=λ
，带人并化简可得：(
-x)
+
=
+(
-y)
，很自然的会得到两组等式：
-x=
λ和
=(
-y)λ，这样便能解出x，y，然后带人4x+y便得到关于λ的式子，可以看成关于λ的函数，求这个函数的最小值即可．
| AE |
| AB |
| ME |
| AC |
| NE |
| ME |
| 1 |
| 4 |
| AB |
| 1 |
| 4 |
| AC |
| NE |
| 1 |
| 4 |
| AB |
| 1 |
| 4 |
| AC |
| ME |
| NE |
| ME |
| NE |
| 1 |
| 4 |
| AB |
| 1 |
| 4 |
| AC |
| 1 |
| 4 |
| AB |
| 1 |
| 4 |
| AB |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
解答：
解：由题意得：
=x
+
=
(
+
)．
∴
=(
-x)
+
．
同理，
=(
-y)
+
；∵
与
共线，∴存在实数λ，使
=λ
（λ＜0）；
∴(
-x)
+
=(
-y)λ
+
λ
；
∴
，∴
；
∴4x+y=1-λ+
（1-
）=(-λ)+
+
≥1+
=
；
∴4x+y的最小值是
．
故答案为
．
| AE |
| AB |
| ME |
| 1 |
| 4 |
| AB |
| AC |
∴
| ME |
| 1 |
| 4 |
| AB |
| 1 |
| 4 |
| AC |
同理，
| NE |
| 1 |
| 4 |
| AC |
| 1 |
| 4 |
| AB |
| ME |
| NE |
| ME |
| NE |
∴(
| 1 |
| 4 |
| AB |
| 1 |
| 4 |
| AC |
| 1 |
| 4 |
| AC |
| 1 |
| 4 |
| AB |
∴
|
|
∴4x+y=1-λ+
| 1 |
| 4 |
| 1 |
| λ |
| 1 |
| (-4λ) |
| 5 |
| 4 |
| 5 |
| 4 |
| 9 |
| 4 |
∴4x+y的最小值是
| 9 |
| 4 |
故答案为
| 9 |
| 4 |
点评：考查向量的加法运算，共线及共面向量基本定理，基本不等式这几个知识点．求解本题的关键是分别用
，
和
，
来表示向量
，最后用λ分别表示x，y，转化成求关于λ函数的最小值．
| AB |
| ME |
| AC |
| NE |
| AE |
练习册系列答案
名校课堂系列答案
相关题目
复数
+2等于（ ）
| (1+i)4 |
| 1-i |
| A、2-2i | B、-2i |
| C、1-i | D、2i |
如图，已知PA⊥⊙O所在的平面，AB是⊙O的直径，AB=2，C是⊙O上一点，且AC=BC，PC与⊙O所在的平面成45°角，E是PC中点．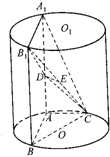
如图，AA1、BB1为圆柱OO1的母线，BC是底面圆O的直径，D、E分别是AA1、CB1的中点，AB=AC．