题目内容
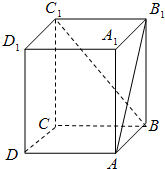
如图:正方体ABCD-A1B1C1D1中,AB1与C1B所成的角为( )

A、
| ||
B、
| ||
C、
| ||
D、
|
考点:异面直线及其所成的角
专题:空间角
分析:连接AD1,BD1,因为几何体是正方体,所以AD1,∥BC1,得到AB1与C1B所成的角为B1AD1,并且△B1AD1,为等边三角形,得到∠B1AD1,为60°.
解答:
解:连接AD1,BD1,
∵几何体是正方体,
∴AD1,∥BC1,
∴AB1与C1B所成的角为∠B1AD1,并且△B1AD1,为等边三角形,
∴∠B1AD1=
;
故选B.
∵几何体是正方体,
∴AD1,∥BC1,
∴AB1与C1B所成的角为∠B1AD1,并且△B1AD1,为等边三角形,
∴∠B1AD1=
| π |
| 3 |
故选B.
点评:本题考查了正方体中异面直线所成的角的求法;关键是正确利用正方体的性质将异面直线所成的角转为平面角,然后关键平面几何的知识求之.

练习册系列答案
相关题目
已知f(x)=ax3+bx-4其中a,b为常数,若f(-2)=7,则f(2)的值等于( )
| A、15 | B、-7 | C、14 | D、-15 |
从正方体ABCD-A1B1C1D1的6个表面中选取3个面,其中有2个面不相邻的选法共有( )
| A、8种 | B、12种 |
| C、16种 | D、20种 |