题目内容
过原点且斜率为-
的直线l1与直线l2:2x+3y-1=0交于A点,求过点A且圆心在直线y=-2x上,并与直线x+y-1=0相切的圆的方程.
| 1 |
| 2 |
考点:圆的切线方程
专题:计算题,直线与圆
分析:求出过原点且斜率为-
的直线l1的方程与2x+3y-1=0联立得A(2,-1),设圆方程为(x-a)2+(y-b)2=r2,圆心(a,b),则-2a=b,
=r,(2-a)2+(-1-b)2=r2,求出a,b,r,即可求出圆的方程.
| 1 |
| 2 |
| |a+b-1| | ||
|
解答:
解:过原点且斜率为-
的直线l1的方程为x+2y=0.
x+2y=0与2x+3y-1=0联立得A(2,-1),
设圆方程为(x-a)2+(y-b)2=r2,圆心(a,b),
则-2a=b,
=r,(2-a)2+(-1-b)2=r2,
解得a=1 b=-2 r=
,
所以圆的方程为(x-1)2+(y+2)2=2.
| 1 |
| 2 |
x+2y=0与2x+3y-1=0联立得A(2,-1),
设圆方程为(x-a)2+(y-b)2=r2,圆心(a,b),
则-2a=b,
| |a+b-1| | ||
|
解得a=1 b=-2 r=
| 2 |
所以圆的方程为(x-1)2+(y+2)2=2.
点评:本题考查圆的方程,考查学生的计算能力,属于中档题.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
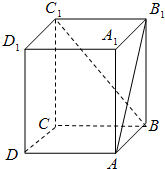
如图:正方体ABCD-A1B1C1D1中,AB1与C1B所成的角为( )

A、
| ||
B、
| ||
C、
| ||
D、
|
某中学拟安排6名实习老师到高一年级的3个班实习,每班2人,则甲在一班、乙不在一班的不同分配方案共有( )
| A、12种 | B、24种 |
| C、36种 | D、48种 |
sin10°cos70°-cos10°sin70°=( )
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|