题目内容
在△ABC中,给出下列5个命题:
(1)若A<B,则sinA<sinB; (2)sinA<sinB若,则A<B;
(3)若A>B,则cot2A>cot2B; (4)若A>B,则cos2A<cos2B;
(5)若A<B,则tan
<tan
;
其中正确命题的序号是 .
(1)若A<B,则sinA<sinB; (2)sinA<sinB若,则A<B;
(3)若A>B,则cot2A>cot2B; (4)若A>B,则cos2A<cos2B;
(5)若A<B,则tan
| A |
| 2 |
| B |
| 2 |
其中正确命题的序号是
考点:命题的真假判断与应用
专题:三角函数的求值
分析:利用正弦定理、三角函数加法定理、倍角公式等知识求解.
解答:
解:在△ABC中:
(1)∵
=
,
∴当A<B时,根据三角形内,大角对大边,得a<b,
∴sinA<sinB,故(1)正确;
(2)∵
=
,
当sinA<sinB时,则a<b,根据三角形内,大边对大角,
∴A<B,故(2)正确;
(3)cot2A-cot2B=
-
=
=
=
,
∵A>B,∴0<A-B<π,
∴sin(B-A)=-sin(A-B)<0,
①当0<A≤
,0<B≤
时,0<2A≤π,0<2B≤π,0≤A-B≤
,
sin2A>0,sin2B>0,cos(B-A)>0
∴cot2A-cot2B<0,∴cot2A<cot2B;
②当
<A<π,0<B≤
时(A和B不可能同时在第二象限),π<2A<2π,0<2B≤π,
∴sin2A<0,sin2B>0
当0≤A-B≤
时,cos(B-A)>0,
∴cot2A-cot2B>0,∴cot2A>cot2B,
当
<A-B≤π时,cos(B-A)<0,
∴cot2A-cot2B<0,∴cot2A<cot2B,
则cot2A>cot2B,故(3)错误;
(4)cos2A-cos2B=
(2cos2A-2cos2B)
=
[(2cos2A-1)-(2cos2B-1)]
=
(cos2A-cos2B)
=
×(-2)×sin(A+B)×sin(A-B)
=-sin(A+B)sin(A-B),
∵A>B,∴0<A-B<π
∵0<A+B<π,∴sin(A+B)>0,
∴cos2A-cos2B<0,cos2A<cos2B.故(4)正确;
(5)tan
-tan
=tan
+tan(-
)
=
,
∵0<
<
,A<B
∴sin
<0,
∵0<
≤
,0<
≤
,
∴tan
-tan
<0,∴tan
<tan
,故(5)正确.
故答案为:(1)(2)(4)(5).
(1)∵
| a |
| sinA |
| b |
| sinB |
∴当A<B时,根据三角形内,大角对大边,得a<b,
∴sinA<sinB,故(1)正确;
(2)∵
| a |
| sinA |
| b |
| sinB |
当sinA<sinB时,则a<b,根据三角形内,大边对大角,
∴A<B,故(2)正确;
(3)cot2A-cot2B=
| cos2A |
| sin2A |
| cos2B |
| sin2B |
=
| cos2Asin2B-cos2Bsin2A |
| sin2Asin2B |
=
| sin2(B-A) |
| sin2Asin2B |
=
| 2sin(B-A)cos(B-A) |
| sin2Asin2B |
∵A>B,∴0<A-B<π,
∴sin(B-A)=-sin(A-B)<0,
①当0<A≤
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
sin2A>0,sin2B>0,cos(B-A)>0
∴cot2A-cot2B<0,∴cot2A<cot2B;
②当
| π |
| 2 |
| π |
| 2 |
∴sin2A<0,sin2B>0
当0≤A-B≤
| π |
| 2 |
∴cot2A-cot2B>0,∴cot2A>cot2B,
当
| π |
| 2 |
∴cot2A-cot2B<0,∴cot2A<cot2B,
则cot2A>cot2B,故(3)错误;
(4)cos2A-cos2B=
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
=-sin(A+B)sin(A-B),
∵A>B,∴0<A-B<π
∵0<A+B<π,∴sin(A+B)>0,
∴cos2A-cos2B<0,cos2A<cos2B.故(4)正确;
(5)tan
| A |
| 2 |
| B |
| 2 |
| A |
| 2 |
| B |
| 2 |
=
sin
| ||||
cos
|
∵0<
| B-A |
| 2 |
| π |
| 2 |
∴sin
| A-B |
| 2 |
∵0<
| A |
| 2 |
| π |
| 2 |
| B |
| 2 |
| π |
| 2 |
∴tan
| A |
| 2 |
| B |
| 2 |
| A |
| 2 |
| B |
| 2 |
故答案为:(1)(2)(4)(5).
点评:本题考查命题真假的判断,解题时要认真审题,注意正弦定理、三角函数加法定理、倍角公式等知识的合理运用.

练习册系列答案
相关题目
下列四个命题中,错误的是( )
A、已知函数f(x)=
| ||
B、设回归直线方程为
| ||
| C、已知ξ服从正态分布 N(0,σ2),且P(-2≤ξ≤0)=0.4,则P(ξ>2)=0.1 | ||
| D、对于命题p:“?x∈R,x2+x+1<0”,则?p:“?x∈R,x2+x+1>0” |
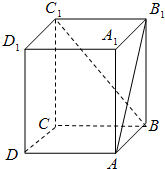
如图:正方体ABCD-A1B1C1D1中,AB1与C1B所成的角为( )

A、
| ||
B、
| ||
C、
| ||
D、
|
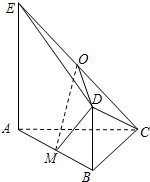 如图,平面ABDE⊥平面ABC,△ABC是等腰直角三角形,AC=BC=4,四边形ABDE是直角梯形,BD∥AE,BD⊥AB,BD=
如图,平面ABDE⊥平面ABC,△ABC是等腰直角三角形,AC=BC=4,四边形ABDE是直角梯形,BD∥AE,BD⊥AB,BD=