题目内容
已知函数f（x）=
，x∈[1，3]，若对定义域内任意实数x1，x2，x3，不等式f（x1）+f（x2）＞f（x3）恒成立，则正数k的取值范围是 ．
| x2+4x+k2 |
| x |
考点：函数恒成立问题
专题：
分析：把已知的函数解析式化简变形，得到f（x）=x+
+4．然后对k分类求出函数f（x）的值域，结合对定义域内任意实数x1，x2，x3，
不等式f（x1）+f（x2）＞f（x3）恒成立，转化值域间的关系列不等式求解k的取值范围．
| k2 |
| x |
不等式f（x1）+f（x2）＞f（x3）恒成立，转化值域间的关系列不等式求解k的取值范围．
解答：
解：f（x）=
=x+
+4．
当0＜k＜1时，函数f（x）在[1，3]上为增函数，函数的值域为[k2+5，
+7]，
对定义域内任意实数x1，x2，x3，不等式f（x1）+f（x2）＞f（x3）恒成立，
即2（k2+5）≥
+7，
∴0＜k＜1；
当1≤k≤
时，函数f（x）在[1，3]上的值域为[2k+4，
+7]，
对定义域内任意实数x1，x2，x3，不等式f（x1）+f（x2）＞f（x3）恒成立，
即4k+8≥
+7，
∴1≤k≤
；
当
≤k≤3时，函数f（x）在[1，3]上的值域为[2k+4，k2+5]，
对定义域内任意实数x1，x2，x3，不等式f（x1）+f（x2）＞f（x3）恒成立，
即4k+8≥k2+5，
∴
≤k≤3；
当k＞3时，函数f（x）在[1，3]上为减函数，函数的值域为[
+7，k2+5]
对定义域内任意实数x1，x2，x3，不等式f（x1）+f（x2）＞f（x3）恒成立，
即2×(
+7)≥k2+5，
∴3＜k≤3
．
综上，正数k的范围是：（0，3
]．
故答案为：（0，3
]．
| x2+4x+k2 |
| x |
| k2 |
| x |
当0＜k＜1时，函数f（x）在[1，3]上为增函数，函数的值域为[k2+5，
| k2 |
| 3 |
对定义域内任意实数x1，x2，x3，不等式f（x1）+f（x2）＞f（x3）恒成立，
即2（k2+5）≥
| k2 |
| 3 |
∴0＜k＜1；
当1≤k≤
| 3 |
| k2 |
| 3 |
对定义域内任意实数x1，x2，x3，不等式f（x1）+f（x2）＞f（x3）恒成立，
即4k+8≥
| k2 |
| 3 |
∴1≤k≤
| 3 |
当
| 3 |
对定义域内任意实数x1，x2，x3，不等式f（x1）+f（x2）＞f（x3）恒成立，
即4k+8≥k2+5，
∴
| 3 |
当k＞3时，函数f（x）在[1，3]上为减函数，函数的值域为[
| k2 |
| 3 |
对定义域内任意实数x1，x2，x3，不等式f（x1）+f（x2）＞f（x3）恒成立，
即2×(
| k2 |
| 3 |
∴3＜k≤3
| 3 |
综上，正数k的范围是：（0，3
| 3 |
故答案为：（0，3
| 3 |
点评：本题考查了函数恒成立问题，考查了数学转化思想方法，体现了分类讨论的数学思想方法，解答此题的关键在于明确对定义域内任意实数x1，x2，x3，不等式f（x1）+f（x2）＞f（x3）恒成立的意义，是中高档题．
练习册系列答案
相关题目
半径为1cm，中心角为150°的角所对的弧长为（ ）cm．
A、
| ||
B、
| ||
C、
| ||
D、
|
关于x的二次方程（
•
）x2+4（
•
）x+（
•
）=0没有实数根，则向量
与
的夹角的范围为（ ）
| a |
| a |
| a |
| b |
| b |
| b |
| a |
| b |
A、[0，
| ||||
B、[0，
| ||||
C、（
| ||||
D、（
|
已知m是平面α的一条斜线，点A∉α，为l过点A的一条动直线，那么下列情形可能出现的是（ ）
| A、l⊥m且l∥m |
| B、l∥m且l⊥α |
| C、l⊥m且l⊥α |
| D、l∥m且l∥α |
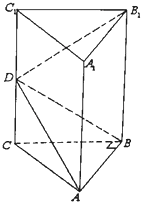如图，在直三棱柱ABC-A1B1C1中，∠ABC=90°，CC1=2AB=2BC=2，D是CC1中点