题目内容
已知复数z=
为实数,i为虚数单位,则实数m的值为 .
| 2-i |
| m+i |
考点:复数代数形式的乘除运算
专题:数系的扩充和复数
分析:利用复数的运算法则、复数为实数的充要条件即可得出.
解答:
解:复数z=
=
=
为实数,
∴
=0,解得m=-2.
故答案为:-2.
| 2-i |
| m+i |
| (2-i)(m-i) |
| (m+i)(m-i) |
| 2m-1-(2+m)i |
| m2+1 |
∴
| -(2+m) |
| m2+1 |
故答案为:-2.
点评:本题考查了复数的运算法则、复数为实数的充要条件,属于基础题.

练习册系列答案
相关题目
已知角α的终边与单位圆相交于点P(
,-
),则sinα=( )
| ||
| 3 |
| ||
| 3 |
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|
函数f(x)=
x3+x-sinx的定义域为R,数列{an}是公差为d的等差数列,且a1+a2+a3+…+a2014<0,记m=f(a1)+f(a2)+f(a3)+…+f(a2014).关于实数m,下列说法正确的是( )
| 1 |
| 3 |
| A、m恒为负数 |
| B、m恒为正数 |
| C、当d>0时,m恒为正数;当d<0时,m恒为负数 |
| D、当d>0时,m恒为负数;当d<0时,m恒为正数 |
向量
=(-1,3),
=(2,-1),则
-2
等于( )
| a |
| b |
| a |
| b |
| A、(-5,5) |
| B、(5,-5) |
| C、(-3,1) |
| D、(1,-1) |
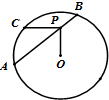 如图,AB是圆O的一条弦,点P是AB上一点,点C是圆O上一点,PC⊥OP,AP=4,PB=2,则PC=
如图,AB是圆O的一条弦,点P是AB上一点,点C是圆O上一点,PC⊥OP,AP=4,PB=2,则PC=