题目内容
若a=sin(sin2012°),b=sin(cos2012°),c=cos(sin2012°),d=cos(cos2012°),则a、b、c、d从小到大的顺序是 .
考点:余弦函数的单调性
专题:计算题,函数的性质及应用
分析:先应用诱导公式化简sin2012°=-sin32°,cos2012°=-cos32°=-sin58°,从而a=-sin(sin32°),b=-sin(sin58°),c=cos(sin32°),d=cos(sin58°),再根据正弦、余弦函数的单调性即可判断a,b,c,d的大小.
解答:
解:∵2012°=5×360°+212°,
∴a=sin(sin2012°)=sin(sin212°)=sin(-sin32°)=-sin(sin32°)<0,
b=sin(cos2012°)=sin(cos212°)=sin(-cos32°)=-sin(cos32°)<0,
c=cos(sin2012°)=cos(sin212°)=cos(-sin32°)=cos(sin32°)>0,
d=cos(cos2012°)=cos(cos212°)=cos(-cos32°)=cos(cos32°)>0,
∵cos32°=sin58°,∴
<sin32°<sin58°<
,
∴c>d,-b>-a,
∴b<a<d<c
故答案为:b<a<d<c.
∴a=sin(sin2012°)=sin(sin212°)=sin(-sin32°)=-sin(sin32°)<0,
b=sin(cos2012°)=sin(cos212°)=sin(-cos32°)=-sin(cos32°)<0,
c=cos(sin2012°)=cos(sin212°)=cos(-sin32°)=cos(sin32°)>0,
d=cos(cos2012°)=cos(cos212°)=cos(-cos32°)=cos(cos32°)>0,
∵cos32°=sin58°,∴
| 1 |
| 2 |
| ||
| 2 |
∴c>d,-b>-a,
∴b<a<d<c
故答案为:b<a<d<c.
点评:本题考查正弦函数、余弦函数的单调性及应用,注意单调区间,同时考查诱导公式的应用,是一道中档题.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
函数f(x)=-x2+2ax+3在区间(-∞,4)上单调递增,则a的取值范围是( )
| A、a<4 | B、a≤4 |
| C、a>4 | D、a≥4 |
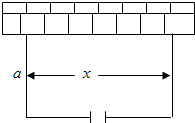 某动物园要围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x(单位:元).
某动物园要围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x(单位:元).