题目内容
证明:-
≤sinα+cosα≤
.
| 2 |
| 2 |
考点:两角和与差的正弦函数
专题:证明题
分析:由两角和与差的正弦函数公式可得sinα+cosα=
(
sinα+
cosα)=
sin(α+
),又-1≤sin(α+
)≤1从而得证.
| 2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
| π |
| 4 |
| π |
| 4 |
解答:
解:sinα+cosα=
(
sinα+
cosα)=
sin(α+
),
∵-1≤sin(α+
)≤1
∴-
≤sinα+cosα≤
.
| 2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
| π |
| 4 |
∵-1≤sin(α+
| π |
| 4 |
∴-
| 2 |
| 2 |
点评:本题主要考察了两角和与差的正弦函数公式的应用,属于基础题.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
已知正方体ABCD-A1B1C1D1,E,F是BD上的动点,是AD1上的动点,则( )
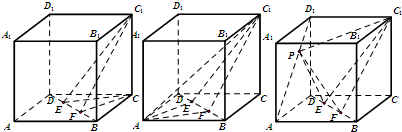

| A、VC-C1EF=VA-C1EF=VP-C1EF |
| B、VC-C1EF=VA-C1EF<VP-C1EF |
| C、VC-C1EF=VA-C1EF>VP-C1EF |
| D、VC-C1EF<VA-C1EF<VP-C1EF |
已知x>1,则函数f(x)=4x+
+1的最小值是( )
| 1 |
| x-1 |
| A、7 | B、9 | C、11 | D、13 |
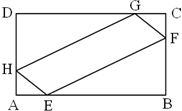 如图所示,在矩形ABCD中,已知AB=a,BC=b(a>b),在AB、AD、CD、CB上分别截取AE、AH、CG、CF都等于x,当x取何值时,四边形EFGH的面积最大?并求出这个最大面积.
如图所示,在矩形ABCD中,已知AB=a,BC=b(a>b),在AB、AD、CD、CB上分别截取AE、AH、CG、CF都等于x,当x取何值时,四边形EFGH的面积最大?并求出这个最大面积.