题目内容
已知△ABC中，sinA+cosA=
，则tanA= ．
| ||
| 5 |
考点：同角三角函数基本关系的运用
专题：三角函数的求值
分析：由条件求得sinAcosA=-
，可得A∈（
，
），故tanA＜-1．再根据sinAcosA=
=-
，求得tanA的值．
| 2 |
| 5 |
| π |
| 2 |
| 3π |
| 4 |
| tanA |
| tan2A+1 |
| 2 |
| 5 |
解答：
解：△ABC中，∵sinA+cosA=
，平方可得sinAcosA=-
＜0，
∴A为钝角，sinA＞0，cosA＜0，且|sinA|＞|cosA|，故A∈（
，
），故tanA＜-1．
再根据sinAcosA=
=
=-
，求得tanA=-2，或 tannA=-
（舍去），
故答案为：-2．
| ||
| 5 |
| 2 |
| 5 |
∴A为钝角，sinA＞0，cosA＜0，且|sinA|＞|cosA|，故A∈（
| π |
| 2 |
| 3π |
| 4 |
再根据sinAcosA=
| sinAcosA |
| sin2A+cos2A |
| tanA |
| tan2A+1 |
| 2 |
| 5 |
| 1 |
| 2 |
故答案为：-2．
点评：本题主要考查根据三角函数值的符号判断角所在的象限，同角三角函数的基本关系，属于基础题．
练习册系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
已知向量
，
，
满足条件
+
+
=0，|
|=|
|=|
|=1，则△P1P2P3是（ ）
| OP1 |
| OP2 |
| OP3 |
| OP1 |
| OP2 |
| OP3 |
| OP1 |
| OP2 |
| OP3 |
| A、等腰三角形 |
| B、等边三角形 |
| C、直角三角形 |
| D、等腰直角三角形 |
已知正方体ABCD-A1B1C1D1，E，F是BD上的动点，是AD1上的动点，则（ ）
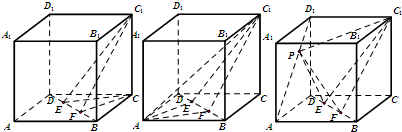
| A、VC-C1EF=VA-C1EF=VP-C1EF |
| B、VC-C1EF=VA-C1EF＜VP-C1EF |
| C、VC-C1EF=VA-C1EF＞VP-C1EF |
| D、VC-C1EF＜VA-C1EF＜VP-C1EF |
已知集合A={a+2，（a+1）2}，若1∈A，则实数a的取值集合为（ ）
| A、{-1，0，-2} |
| B、{-2，0} |
| C、{-2，-1} |
| D、{-1，0} |