题目内容
(1)已知函数y=f(x)的定义域为R,且当x∈R时,f(2+x)=f(2-x)恒成立,求证y=f(x)的图象关于直线x=2对称
(2)若函数y=log2|ax+1|的图象的对称轴是x=2,求非零实数a的值.
(2)若函数y=log2|ax+1|的图象的对称轴是x=2,求非零实数a的值.
考点:函数的图象与图象变化
专题:计算题,函数的性质及应用
分析:(1)设P(x0,y0)是函数y=f(x)图象上任意一点,则y0=f(x0),又P点关于x=2的对称点为Q(4-x0,y0),证明点Q在函数y=f(x)图象上;
(2)由题意,|a(2-x)+1|=|a(2+x)+1|恒成立,即|-ax+(2a+1)|=|xa+(2a+1)|恒成立,从而得2a+1=0.
(2)由题意,|a(2-x)+1|=|a(2+x)+1|恒成立,即|-ax+(2a+1)|=|xa+(2a+1)|恒成立,从而得2a+1=0.
解答:
解:(1)证明:设P(x0,y0)是函数y=f(x)图象上任意一点,则y0=f(x0),
又P点关于x=2的对称点为Q(4-x0,y0),
由已知f(2+x)=f(2-x)可得,
f(4-x0)=f(2+(2-x0))=f(2-(2-x0))=f(x0)=y0,
即Q在函数y=f(x)图象上,
则y=f(x)的图象关于直线x=2对称.
(2)∵对定义域同的任意x,有f(2-x)=f(2+x)恒成立,
∴|a(2-x)+1|=|a(2+x)+1|恒成立,
即|-ax+(2a+1)|=|xa+(2a+1)|恒成立,
又∵a≠0,
∴2a+1=0,
∴a=-
.
又P点关于x=2的对称点为Q(4-x0,y0),
由已知f(2+x)=f(2-x)可得,
f(4-x0)=f(2+(2-x0))=f(2-(2-x0))=f(x0)=y0,
即Q在函数y=f(x)图象上,
则y=f(x)的图象关于直线x=2对称.
(2)∵对定义域同的任意x,有f(2-x)=f(2+x)恒成立,
∴|a(2-x)+1|=|a(2+x)+1|恒成立,
即|-ax+(2a+1)|=|xa+(2a+1)|恒成立,
又∵a≠0,
∴2a+1=0,
∴a=-
| 1 |
| 2 |
点评:本题考查了函数图象对称性的证明与应用,属于基础题.

练习册系列答案
相关题目
已知向量
,
,
满足条件
+
+
=0,|
|=|
|=|
|=1,则△P1P2P3是( )
| OP1 |
| OP2 |
| OP3 |
| OP1 |
| OP2 |
| OP3 |
| OP1 |
| OP2 |
| OP3 |
| A、等腰三角形 |
| B、等边三角形 |
| C、直角三角形 |
| D、等腰直角三角形 |
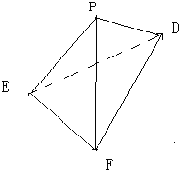 三棱锥P-DEF中,顶点P在平面DEF上的射影为O.
三棱锥P-DEF中,顶点P在平面DEF上的射影为O.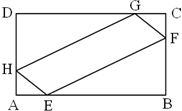 如图所示,在矩形ABCD中,已知AB=a,BC=b(a>b),在AB、AD、CD、CB上分别截取AE、AH、CG、CF都等于x,当x取何值时,四边形EFGH的面积最大?并求出这个最大面积.
如图所示,在矩形ABCD中,已知AB=a,BC=b(a>b),在AB、AD、CD、CB上分别截取AE、AH、CG、CF都等于x,当x取何值时,四边形EFGH的面积最大?并求出这个最大面积.