题目内容
已知向量
，
，
满足条件
+
+
=0，|
|=|
|=|
|=1，则△P1P2P3是（ ）
| OP1 |
| OP2 |
| OP3 |
| OP1 |
| OP2 |
| OP3 |
| OP1 |
| OP2 |
| OP3 |
| A、等腰三角形 |
| B、等边三角形 |
| C、直角三角形 |
| D、等腰直角三角形 |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：首先，根据
+
+
=
，得到∠P1OP2=120°，然后，结合|
|=|
|=|
|=1，得到|P1P2|=|P2P3|=|P1P3|，从而得到结果．
| OP1 |
| OP2 |
| OP3 |
| 0 |
| OP1 |
| OP2 |
| OP3 |
解答：
解：∵
+
+
=
，
∴
+
=-
（
+
）2=（-
）2
|
|2+2
•
+|
|2=|
|2
∴cos∠P1OP2=-
，
∴∠P1OP2=120°
同理：∠P1OP3=∠P2OP3=120°
又|
|=|
|=|
|=1，
可得|P1P2|=|P2P3|=|P1P3|
故△P1P2P3是等边三角形，
故选：B．
| OP1 |
| OP2 |
| OP3 |
| 0 |
∴
| OP1 |
| OP2 |
| OP3 |
（
| OP1 |
| OP2 |
| OP3 |
|
| OP1 |
| OP1 |
| OP2 |
| OP2 |
| OP3 |
∴cos∠P1OP2=-
| 1 |
| 2 |
∴∠P1OP2=120°
同理：∠P1OP3=∠P2OP3=120°
又|
| OP1 |
| OP2 |
| OP3 |
可得|P1P2|=|P2P3|=|P1P3|
故△P1P2P3是等边三角形，
故选：B．
点评：本题重点考查了平面向量的基本运算和数量积的运算律，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
利用计算机产生0～1之间的群与随机数a，则事件-
＜3a-1＜0发生的概率为（ ）
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
如图是调查某地某公司1000名员工的月收入后制作的直方图．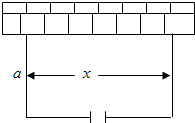
某动物园要围建一个面积为360m2的矩形场地，要求矩形场地的一面利用旧墙（利用旧墙需维修），其它三面围墙要新建，在旧墙的对面的新墙上要留一个宽度为2m的进出口，如图所示，已知旧墙的维修费用为45元/m，新墙的造价为180元/m，设利用的旧墙的长度为x（单位：元）．