题目内容
已知圆C的极坐标方程为ρ=2,以极点为原点,极轴为x轴的正半轴建立平面直角坐标系,若直线l:kx+y+3=0与圆C相切.
求(1)圆C的直角坐标方程;
(2)实数k的值.
求(1)圆C的直角坐标方程;
(2)实数k的值.
考点:简单曲线的极坐标方程
专题:坐标系和参数方程
分析:(1)根据题意和ρ2=x2+y2把极坐标方程化为直角坐标方程即可;
(2)根据直线和圆相切的性质:圆心到直线的距离等于半径,利用点到直线的距离公式列出方程求出k的值.
(2)根据直线和圆相切的性质:圆心到直线的距离等于半径,利用点到直线的距离公式列出方程求出k的值.
解答:
解:(1)由题意得,圆C的极坐标方程为ρ=2,则ρ2=4,
所以圆C的直角坐标方程是:x2+y2=4…(5分)
(2)因为直线l:kx+y+3=0与圆C相切,
所以
=2,解得k=±
…(10分)
所以圆C的直角坐标方程是:x2+y2=4…(5分)
(2)因为直线l:kx+y+3=0与圆C相切,
所以
| |3| | ||
|
| ||
| 2 |
点评:本题主要考查把极坐标方程、参数方程化为直角坐标方程的方法,点到直线的距离公式的应用,直线和圆的位置关系,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知一个棱长为2的正方体,被一个平面截后所得几何体的三视图如图所示,则该几何体的体积是( )


| A、7 | ||
B、
| ||
C、
| ||
D、
|
已知向量
,
,
满足条件
+
+
=0,|
|=|
|=|
|=1,则△P1P2P3是( )
| OP1 |
| OP2 |
| OP3 |
| OP1 |
| OP2 |
| OP3 |
| OP1 |
| OP2 |
| OP3 |
| A、等腰三角形 |
| B、等边三角形 |
| C、直角三角形 |
| D、等腰直角三角形 |
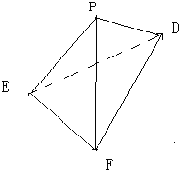 三棱锥P-DEF中,顶点P在平面DEF上的射影为O.
三棱锥P-DEF中,顶点P在平面DEF上的射影为O.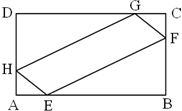 如图所示,在矩形ABCD中,已知AB=a,BC=b(a>b),在AB、AD、CD、CB上分别截取AE、AH、CG、CF都等于x,当x取何值时,四边形EFGH的面积最大?并求出这个最大面积.
如图所示,在矩形ABCD中,已知AB=a,BC=b(a>b),在AB、AD、CD、CB上分别截取AE、AH、CG、CF都等于x,当x取何值时,四边形EFGH的面积最大?并求出这个最大面积.