题目内容
2.在等差数列{an}中,a2=3,a5=12,则a8=21.分析 由等差数列的性质可得a2+a8=2a5,代入数据计算可得答案.
解答 解:由等差数列的性质可得a2+a8=2a5,
代入数据可得3+a8=2×12,
解得a8=21;
故答案为:21.
点评 本题考查等差数列的性质,关键是熟练运用等差数列的性质进行分析.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
12.在同一坐标系中,函数y=-2x与y=-$\frac{3}{x}$的图象的交点在( )
| A. | 第一,三象限 | B. | 第二,四象限 | C. | 第四象限 | D. | 不存在 |
5.双曲线a2x2-$\frac{a}{3}$y2=1的一个焦点是(-2,0),则a等于( )
| A. | -$\frac{1}{4}$ | B. | 1 | C. | -$\frac{1}{4}$或1 | D. | $\frac{1}{4}$或-1 |
3.如果双曲线经过点P(2,$\sqrt{2}$),且它的一条渐近线方程为y=x,那么该双曲线的方程是( )
| A. | x2-$\frac{3{y}^{2}}{2}$=1 | B. | $\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{2}$=1 | C. | $\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{6}$=1 | D. | $\frac{{y}^{2}}{2}$-$\frac{{x}^{2}}{2}$=1 |
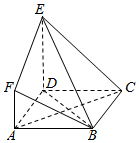 如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°.
如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°.