Question

2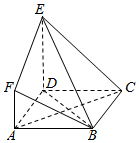．如图，ABCD是边长为3的正方形，DE⊥平面ABCD，AF∥DE，DE=3AF，BE与平面ABCD所成角为60°．
（1）求证：AC⊥平面BDE；
（2）求V_B-FADE的大小．

Answer 1

分析 （1）由底面正方形可知AC⊥BD，由DE⊥平面ABCD可得DE⊥AC，故而AC⊥平面BDE；
（2）由∠DBE=60°可求得DE，进而计算AF，由题意可易证AB⊥平面ADEF，故而V=$\frac{1}{3}{S}_{梯形ADEF}•AB$．

解答 解：（1）证明：∵DE⊥平面ABCD，AC?平面ABCD，
∴DE⊥AC． 
∵ABCD是正方形，
∴AC⊥BD．又BD?平面BDE，DE?平面BDE，BD∩DE=D，
∴AC⊥平面BDE．
（2）∵DE⊥平面ABCD，∴∠DBE为BE与平面ABCD所成角，即∠DBE=60°，
∵ABCD是边长为3的正方形，
∴BD=3$\sqrt{2}$，∵DE=BDtan60°=3$\sqrt{6}$，AF=$\sqrt{6}$．
∵DE⊥平面ABCD，DE?平面ADEF，
∴平面ADEF⊥平面ABCD，又平面ADEF∩平面ABCD=AD，AD⊥AB，AB?平面ABCD，
∴AB⊥平面ADEF．
V_B-FADE=$\frac{1}{3}$S_梯形ABEF•AB=$\frac{1}{3}•\frac{1}{2}$（AF+ED）•AD•AB=$\frac{1}{6}$（$\sqrt{6}$+3$\sqrt{6}$）•3•3=6$\sqrt{6}$．

点评 本题考查了线面垂直的判定与性质，棱锥的体积计算，属于中档题．