题目内容
3.如果双曲线经过点P(2,$\sqrt{2}$),且它的一条渐近线方程为y=x,那么该双曲线的方程是( )| A. | x2-$\frac{3{y}^{2}}{2}$=1 | B. | $\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{2}$=1 | C. | $\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{6}$=1 | D. | $\frac{{y}^{2}}{2}$-$\frac{{x}^{2}}{2}$=1 |
分析 由双曲线的一条渐近线方程为y=x,可设双曲线的方程为x2-y2=λ(λ≠0),代入点P(2,$\sqrt{2}$),解方程即可得到所求双曲线的方程.
解答 解:由双曲线的一条渐近线方程为y=x,
可设双曲线的方程为x2-y2=λ(λ≠0),
代入点P(2,$\sqrt{2}$),可得
λ=4-2=2,
可得双曲线的方程为x2-y2=2,
即为$\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{2}$=1.
故选:B.
点评 本题考查双曲线的方程的求法,注意运用渐近线方程和双曲线的方程的关系,考查运算能力,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
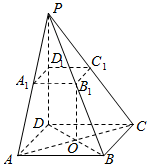 在四棱锥P-ABCD中,底面ABCD是菱形,PD⊥平面ABCD,点D1为棱PD的中点,过D1作与平面ABCD平行的平面与棱PA,PB,PC相交于A1,B1,C1,∠BAD=60°.
在四棱锥P-ABCD中,底面ABCD是菱形,PD⊥平面ABCD,点D1为棱PD的中点,过D1作与平面ABCD平行的平面与棱PA,PB,PC相交于A1,B1,C1,∠BAD=60°.