题目内容
17.已知α∈(0,$\frac{π}{2}$),cosα=$\frac{3}{5}$.(1)求sin($\frac{π}{6}$+α)的值;
(2)求cos($\frac{π}{3}$+2α)的值.
分析 (1)由题意和同角三角函数基本关系可得sinα,代入sin($\frac{π}{6}$+α)=$\frac{1}{2}$cosα+$\frac{\sqrt{3}}{2}$sinα,计算可得;
(2)由(1)和二倍角公式可得sin2α和cos2α,代入cos($\frac{π}{3}$+2α)=$\frac{1}{2}$cos2α-$\frac{\sqrt{3}}{2}$sin2α,计算可得.
解答 解:(1)∵α∈(0,$\frac{π}{2}$),cosα=$\frac{3}{5}$,
∴sinα=$\sqrt{1-co{s}^{2}α}$=$\frac{4}{5}$,
∴sin($\frac{π}{6}$+α)=$\frac{1}{2}$cosα+$\frac{\sqrt{3}}{2}$sinα
=$\frac{1}{2}$×$\frac{3}{5}$+$\frac{\sqrt{3}}{2}$×$\frac{4}{5}$=$\frac{3+4\sqrt{3}}{10}$;
(2)由(1)可得sin2α=2sinαcosα=$\frac{24}{25}$,
cos2α=cos2α-sin2α=-$\frac{7}{25}$,
∴cos($\frac{π}{3}$+2α)=$\frac{1}{2}$cos2α-$\frac{\sqrt{3}}{2}$sin2α
=$\frac{1}{2}$×(-$\frac{7}{25}$)-$\frac{\sqrt{3}}{2}$×$\frac{24}{25}$=-$\frac{7+24\sqrt{3}}{50}$
点评 本题考查和差角的三角函数公式,涉及二倍角公式和同角三角函数基本关系,属基础题.

练习册系列答案
 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
17.与双曲线$\frac{y^2}{4}-\frac{x^2}{3}=1$共同的渐近线,且过点(-3,2)的双曲线的标准方程是( )
| A. | $\frac{y^2}{8}-\frac{x^2}{6}=1$ | B. | $\frac{x^2}{6}-\frac{y^2}{8}=1$ | C. | $\frac{x^2}{16}-\frac{y^2}{9}=1$ | D. | $\frac{y^2}{9}-\frac{x^2}{16}=1$ |
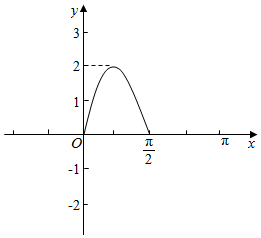 已知函数f(x)=2sinωx(ω>0)的部分图象如图所示.
已知函数f(x)=2sinωx(ω>0)的部分图象如图所示.