题目内容
5.双曲线a2x2-$\frac{a}{3}$y2=1的一个焦点是(-2,0),则a等于( )| A. | -$\frac{1}{4}$ | B. | 1 | C. | -$\frac{1}{4}$或1 | D. | $\frac{1}{4}$或-1 |
分析 根据双曲线的焦点坐标建立方程关系进行求解即可.
解答 解:双曲线的标准方程为$\frac{{x}^{2}}{\frac{1}{{a}^{2}}}-\frac{{y}^{2}}{\frac{3}{a}}$=1,
∵双曲线a2x2-$\frac{a}{3}$y2=1的一个焦点是(-2,0),
∴c=2,且$\frac{3}{a}$>0,
则a>0,且$\frac{1}{{a}^{2}}$+$\frac{3}{a}$=c2=4,
即4a2-3a-1=0,
得a=1或a=-$\frac{1}{4}$(舍),
故选:B.
点评 本题主要考查双曲线的方程和性质,根据双曲线的焦点坐标建立方程关系是解决本题的关键.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
17.与双曲线$\frac{y^2}{4}-\frac{x^2}{3}=1$共同的渐近线,且过点(-3,2)的双曲线的标准方程是( )
| A. | $\frac{y^2}{8}-\frac{x^2}{6}=1$ | B. | $\frac{x^2}{6}-\frac{y^2}{8}=1$ | C. | $\frac{x^2}{16}-\frac{y^2}{9}=1$ | D. | $\frac{y^2}{9}-\frac{x^2}{16}=1$ |
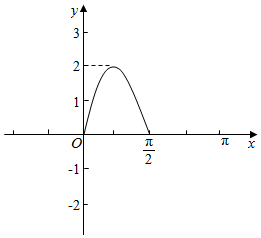 已知函数f(x)=2sinωx(ω>0)的部分图象如图所示.
已知函数f(x)=2sinωx(ω>0)的部分图象如图所示.