题目内容
设2x=5y=m,且
+
=2,则m的值是 .
| 1 |
| x |
| 1 |
| y |
考点:对数的运算性质
专题:计算题,不等式的解法及应用
分析:化指数式为对数式,把x,y用含有m的代数式表示,代入
+
=2,然后利用对数的运算性质求解m的值.
| 1 |
| x |
| 1 |
| y |
解答:
解:由2x=5y=m,
得x=log2m,y=log5m,
由
+
=2,得
+
=2,
即logm2+logm5=2,
∴logm10=2,
∴m=
.
故答案为:
.
得x=log2m,y=log5m,
由
| 1 |
| x |
| 1 |
| y |
| 1 |
| log2m |
| 1 |
| log5m |
即logm2+logm5=2,
∴logm10=2,
∴m=
| 10 |
故答案为:
| 10 |
点评:本题考查了指数式和对数式的互化,考查了对数的运算性质,是基础的计算题.

练习册系列答案
相关题目
在△ABC中,三边长分别为a,b,c,且A=30°,B=45°,a=1,则b的值是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
将一颗骰子连续抛掷三次,已知它落地时向上的点数恰好依次成等差数列,那么这三次抛掷向上的点数之和为12的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,已知椭圆C:
如图,已知椭圆C: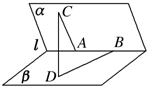 如图,在45°的二面角α-l-β的棱上有两点A、B,点C、D分别在平面 α、β内,且AC⊥AB,DB⊥AB,AC=BD=AB=1,则CD的长度为
如图,在45°的二面角α-l-β的棱上有两点A、B,点C、D分别在平面 α、β内,且AC⊥AB,DB⊥AB,AC=BD=AB=1,则CD的长度为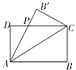 某制冷设备厂设计生产一种长方形薄板,如图所示,长方形ABCD(AB>AD)的周长为4米,沿AC折叠使B到B′位置,AB′交DC于P.研究发现当ADP的面积最大时最节能,则最节能时长方形ABCD的面积为
某制冷设备厂设计生产一种长方形薄板,如图所示,长方形ABCD(AB>AD)的周长为4米,沿AC折叠使B到B′位置,AB′交DC于P.研究发现当ADP的面积最大时最节能,则最节能时长方形ABCD的面积为