题目内容
点A时椭圆
+
=1上的一个动点,点P在线段OA的延长上且
•
=48.则点P的横坐标的最大值是 .
| x2 |
| 25 |
| y2 |
| 9 |
| OA |
| OP |
考点:椭圆的简单性质
专题:综合题,圆锥曲线的定义、性质与方程
分析:根据向量共线定理设
=λ
(λ>1),结合题意算出λ=
.设A(x,y)、P(m,n),由向量的坐标运算公式,化简得m=λx═
,再利用基本不等式求最值,可得P点横坐标的最大值.
| OP |
| OA |
| 48 | ||
|
|
| 48 | ||||
|
解答:
解:∵点P在线段OA的延长线上,
∴设
=λ
(λ>1),
由
•
=48得λ|
|2=48,可得λ=
.
设A(x,y),P(m,n),则
m=λx=
•x=
•x=
≤
=10,
由此可得:当且仅当
=
x,即A点横坐标x=
时,P点横坐标的最大值为10.
故答案为:10.
∴设
| OP |
| OA |
由
| OA |
| OP |
| OA |
| 48 | ||
|
|
设A(x,y),P(m,n),则
m=λx=
| 48 | ||
|
|
| 48 |
| x2+y2 |
| 48 | ||||
|
| 48 | ||||||
2
|
由此可得:当且仅当
| 9 |
| x |
| 16 |
| 25 |
| 15 |
| 4 |
故答案为:10.
点评:本题已知椭圆上的动点满足的条件,求点P横坐标的最大值.着重考查了向量的数量积及其运算性质、向量的坐标运算公式、基本不等式与椭圆的简单几何性质等知识,属于中档题.

练习册系列答案
相关题目
设函数f(x)=
,则f(log23)=( )
|
|
| A、13 | B、19 | C、37 | D、49 |
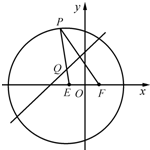 如图,已知圆E:(x+1)2+y2=16,点F(1,0),P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q.
如图,已知圆E:(x+1)2+y2=16,点F(1,0),P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q.