题目内容

在△ABC中，三边长分别为a，b，c，且A=30°，B=45°，a=1，则b的值是（　　）
A、
1
2
B、
2
2
C、
2
D、
6
2
考点：正弦定理
专题：计算题,解三角形
分析：由正弦定理可得
1
sin30°
=
b
sin45°
，即可得出结论．
解答： 解：∵三边长分别为a，b，c，且A=30°，B=45°，a=1，
∴由正弦定理可得
1
sin30°
=
b
sin45°
，
∴b=
2
．
故选：C．
点评：本题考查正弦定理，考查学生的计算能力，属于基础题．
练习册系列答案
相关题目
如图所示程序框图，则输出的s的值为
 
．
设2x=5y=m，且
1
x
+
1
y
=2，则m的值是
 
．
双曲线
x2
4
-
y2
5
=1的渐近线方程为
 
．
已知函数f（x）=
-x2+x，x≤1
log
1
3
x，x＞1
，若对任意的x∈R，不等式f（x）≤m2-
3
4
m恒成立，则实数m的取值范围为
 
．
已知函数f（x）=log2x与函数g（x）的图象关于y=x对称，且有g（a）g（b）=2，a＞0，b＞0，则
4
a
+
1
b
的最小值为（　　）
A、9
B、
9
4
C、4
D、5
圆（x-1）2+y2=3的圆心坐标和半径分别是（　　）
A、（-1，0），3
B、（1，0），3
C、(-1，0)，
3
D、(1，0)，
3
已知函数f（x）=
ex+m
ex+1
，若?a，b，c∈R，f（a），f（b），f（c）为某一个三角形的边长，则实数m的取值范围是（　　）
A、[
1
2
，1]
B、[0，1]
C、[1，2]
D、[
1
2
，2]
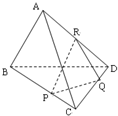（理科）已知如图，四面体ABCD中，P，Q，R分别在棱BC，CD，DA上，且BP=2PC，CQ=2QD，DR=RA，则A，B两点到平面PQR的距离之比为（　　）
A、1：4B、1：3
C、1：2D、1：1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网