题目内容
 如图,已知椭圆C:
如图,已知椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 1 |
| 2 |
(1)求椭圆C的方程;
(2)求
| TM |
| TN |
(3)设点P是椭圆C上异于M,N的任意一点,且直线MP,NP分别与x轴交于点R,S,O为坐标原点,问丨OR丨•丨OS丨是否为定值?若是请求出定值,不是则说明理由.
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)依题意,得a=2,根据椭圆C:
+
=1(a>b>0)经过点(
,
),求出b,由此能求出椭圆C的方程.
(2)点M与点N关于x轴对称,设M(x1,y1),N(x1,-y1),设y1>0.由于点M在椭圆C上,故y12=1-
.由T(-2,0),知
•
=(x1+2,y1)•(x1+2,-y1)=
(x1+
)2-
,由此能求出圆T的方程.
(3)设P(x0,y0),则直线MP的方程为:y-y0=
(x-x0),令y=0,得xR=
,同理:xS=
,故xRxS=
,由此能够证明|OR|•|OS|=|xR|•|xS|=|xR•xS|=4为定值.
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 1 |
| 2 |
(2)点M与点N关于x轴对称,设M(x1,y1),N(x1,-y1),设y1>0.由于点M在椭圆C上,故y12=1-
| x12 |
| 4 |
| TM |
| TN |
| 5 |
| 4 |
| 8 |
| 5 |
| 1 |
| 5 |
(3)设P(x0,y0),则直线MP的方程为:y-y0=
| y0-y1 |
| x0-x1 |
| x1y0-x0y1 |
| y0-y1 |
| x1y0+x0y1 |
| y0+y1 |
| x12y02-x02y12 |
| y02-y12 |
解答:
解:(1)依题意,得a=2,
∵椭圆C:
+
=1(a>b>0)经过点(
,
),
∴
+
=1,
∴b=1,
故椭圆C的方程为
+y2=1.
(2)点M与点N关于x轴对称,
设M(x1,y1),N(x1,-y1),不妨设y1>0.
由于点M在椭圆C上,所以y12=1-
. (*)
由已知T(-2,0),则
=(x1+2,y1),
=(x1+2,-y1),
∴
•
=(x1+2,y1)•(x1+2,-y1)=(x1+2)2-y12
=
x12+4x1+3=
(x1+
)2-
.
由于-2<x1<2,故当x1=
时,
•
取得最小值为-
.
(3)设P(x0,y0),则直线MP的方程为:y-y0=
(x-x0),
令y=0,得xR=
,同理:xS=
,
故xRxS=
(**)
又点M与点P在椭圆上,故x02=4(1-y02),x12=4(1-y12),
代入(**)式,得:xRxS=4.
∴OR|•|OS|=|xR|•|xS|=|xR•xS|=4为定值.
∵椭圆C:
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 1 |
| 2 |
∴
| 3 |
| 4 |
| ||
| b2 |
∴b=1,
故椭圆C的方程为
| x2 |
| 4 |
(2)点M与点N关于x轴对称,
设M(x1,y1),N(x1,-y1),不妨设y1>0.
由于点M在椭圆C上,所以y12=1-
| x12 |
| 4 |
由已知T(-2,0),则
| TM |
| TN |
∴
| TM |
| TN |
=
| 5 |
| 4 |
| 5 |
| 4 |
| 8 |
| 5 |
| 1 |
| 5 |
由于-2<x1<2,故当x1=
| 8 |
| 5 |
| TM |
| TN |
| 1 |
| 5 |
(3)设P(x0,y0),则直线MP的方程为:y-y0=
| y0-y1 |
| x0-x1 |
令y=0,得xR=
| x1y0-x0y1 |
| y0-y1 |
| x1y0+x0y1 |
| y0+y1 |
故xRxS=
| x12y02-x02y12 |
| y02-y12 |
又点M与点P在椭圆上,故x02=4(1-y02),x12=4(1-y12),
代入(**)式,得:xRxS=4.
∴OR|•|OS|=|xR|•|xS|=|xR•xS|=4为定值.
点评:本题考查椭圆的方程和几何性质、圆的方程等基础知识,考查运算求解能力、推理论证能力,考查函数与方程思想、数形结合思想.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
设z=1-i(i是虚数单位),则复数
的虚部是( )
| 2 |
| z |
| A、1 | B、-1 | C、i | D、-i |
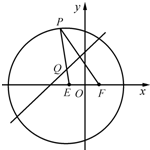 如图,已知圆E:(x+1)2+y2=16,点F(1,0),P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q.
如图,已知圆E:(x+1)2+y2=16,点F(1,0),P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q.