题目内容
将一颗骰子连续抛掷三次,已知它落地时向上的点数恰好依次成等差数列,那么这三次抛掷向上的点数之和为12的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:古典概型及其概率计算公式
专题:概率与统计
分析:将一颗骰子连续抛掷三次,落地时向上的点数恰好依次成等差数列的情况有18种,其中三次抛掷向上的点数之和为12的有5种.根据古典概型的概率计算公式即可求出三次抛掷向上的点数之和为12的概率为
.
| 5 |
| 18 |
解答:
解:将一颗骰子连续抛掷三次,
落地时向上的点数恰好依次成等差数列的情况有
公差为0:(1,1,1),(2,2,2),(3,3,3),(4,4,4),(5,5,5),(6,6,6)共6种.
公差为1:(1,2,3),(2,3,4),(3,4,5),(4,5,6).共4种;
同理,公差为-1的有4种.
公差为2:(1,3,5),(2,4,6),共2种;
同理公差为-2的有2种.
所有共有18种.
其中,三次抛掷向上的点数之和为12的有:
(4,4,4),(3,4,5),(5,4,3),(2,4,6),(6,4,2)共5种.
∴三次抛掷向上的点数之和为12的概率为
.
故选:A.
落地时向上的点数恰好依次成等差数列的情况有
公差为0:(1,1,1),(2,2,2),(3,3,3),(4,4,4),(5,5,5),(6,6,6)共6种.
公差为1:(1,2,3),(2,3,4),(3,4,5),(4,5,6).共4种;
同理,公差为-1的有4种.
公差为2:(1,3,5),(2,4,6),共2种;
同理公差为-2的有2种.
所有共有18种.
其中,三次抛掷向上的点数之和为12的有:
(4,4,4),(3,4,5),(5,4,3),(2,4,6),(6,4,2)共5种.
∴三次抛掷向上的点数之和为12的概率为
| 5 |
| 18 |
故选:A.
点评:本题考查古典概型及概率计算公式等知识,属于基础题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
圆(x-1)2+y2=3的圆心坐标和半径分别是( )
| A、(-1,0),3 | ||
| B、(1,0),3 | ||
C、(-1,0),
| ||
D、(1,0),
|
已知函数f(x)=
,若?a,b,c∈R,f(a),f(b),f(c)为某一个三角形的边长,则实数m的取值范围是( )
| ex+m |
| ex+1 |
A、[
| ||
| B、[0,1] | ||
| C、[1,2] | ||
D、[
|
设函数f(x)=
,则f(log23)=( )
|
|
| A、13 | B、19 | C、37 | D、49 |
已知向量
=(1,2),
=(2,1),则(
•
)(
-2
)等于( )
| m |
| n |
| m |
| n |
| m |
| n |
| A、(-12,0) | B、4 |
| C、(-3,0) | D、-12 |
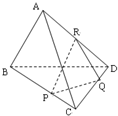 (理科)已知如图,四面体ABCD中,P,Q,R分别在棱BC,CD,DA上,且BP=2PC,CQ=2QD,DR=RA,则A,B两点到平面PQR的距离之比为( )
(理科)已知如图,四面体ABCD中,P,Q,R分别在棱BC,CD,DA上,且BP=2PC,CQ=2QD,DR=RA,则A,B两点到平面PQR的距离之比为( )| A、1:4 | B、1:3 |
| C、1:2 | D、1:1 |