Question

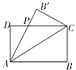某制冷设备厂设计生产一种长方形薄板，如图所示，长方形ABCD（AB＞AD）的周长为4米，沿AC折叠使B到B′位置，AB′交DC于P．研究发现当ADP的面积最大时最节能，则最节能时长方形ABCD的面积为

 

．

Answer 1

考点：基本不等式

专题：不等式的解法及应用

分析：设AB=x，DP=y，BC=2-x，PC=x-y．利用x＞2-x，可得x的取值范围．利用△ADP≌△CB′P，可得PA=PC=x-y．利用勾股定理可得PA²=AD²+DP²，得到y=2（1-

1

x

），1＜x＜2．记△ADP的面积为S₁，利用基本不等式可得S₁=（1-

1

x

）（2-x）=3-（x+

2

x

）≤3-2

2

，当且仅当x=

2

∈（1，2）时，S₁取得最大值，进而得到长方形ABCD的面积S₂=x（2-x）=

2

（2-

2

）=2

2

-2．

解答： 解：设AB=x，DP=y，BC=2-x，PC=x-y．
∵x＞2-x，∴1＜x＜2，
∵△ADP≌△CB′P，∴PA=PC=x-y．
由PA²=AD²+DP²，得（x-y）²=（2-x）²+y²，
∴y=2（1-

1

x

），1＜x＜2，
记△ADP的面积为S₁，
则S₁=（1-

1

x

）（2-x）=3-（x+

2

x

）≤3-2

2

，
当且仅当x=

2

∈（1，2）时，S₁取得最大值，
此时长方形ABCD的面积S₂=x（2-x）=

2

（2-

2

）=2

2

-2．
故答案为：2

2

-2．

点评：本题综合考查了全等三角形的判定与性质、勾股定理、基本不等式等基础知识与基本技能方法，属于中档题．