题目内容
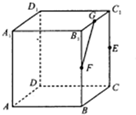 如图,正方体ABCD-A1B1C1D1的棱长为1,E、F、G分别是棱CC1、BB1、B1C1的中点,H是线段FG上一动点,则下列命题正确的是
如图,正方体ABCD-A1B1C1D1的棱长为1,E、F、G分别是棱CC1、BB1、B1C1的中点,H是线段FG上一动点,则下列命题正确的是①A1H与D1E所在的直线是异面直线;
②A1H∥平面D1AE;
③三棱锥H-ABC1的体积为定值
| 1 |
| 12 |
④BC1可能垂直于平面A1HC;
⑤记A1H与平面BCC1B1所成的角为θ,则2≤tanθ≤2
| 2 |
考点:命题的真假判断与应用
专题:空间位置关系与距离,简易逻辑
分析:举反例说明①错误;利用两平面平行的性质说明②正确;由等积法求出三棱锥H-ABC1的体积说明③正确;举特例说明④正确;找出A1H与平面BCC1B1所成的角,在直角三角形中利用角的正切值等于对边除以临边求得tanθ的范围说明⑤正确.
解答:
解:当H与F重合时,A1H∥D1E,故①错误;
由图易知平面A1FG∥平面D1AE,
∴A1H∥平面D1AE,故②正确;
∵FG∥BC1,AB⊥平面HBC1,VHABC1=VAHBC1,
∴三棱锥H-ABC1的体积为定值
,故③正确;
当H是FG的中点时,BC1⊥平面A1HC,故④正确;
∵A1B1⊥平面BCC1B1,∴A1H在平面BCC1B1内的射影为B1H.
故tanθ=
,
由于H点在线段FG上,则B1H∈[
,
],
∴2≤tanθ≤2
.故⑤正确.
∴正确的命题是②③④⑤.
故答案为:②③④⑤
由图易知平面A1FG∥平面D1AE,
∴A1H∥平面D1AE,故②正确;
∵FG∥BC1,AB⊥平面HBC1,VHABC1=VAHBC1,
∴三棱锥H-ABC1的体积为定值
| 1 |
| 12 |
当H是FG的中点时,BC1⊥平面A1HC,故④正确;
∵A1B1⊥平面BCC1B1,∴A1H在平面BCC1B1内的射影为B1H.
故tanθ=
| 1 |
| B1H |
由于H点在线段FG上,则B1H∈[
| ||
| 4 |
| 1 |
| 2 |
∴2≤tanθ≤2
| 2 |
∴正确的命题是②③④⑤.
故答案为:②③④⑤
点评:本题考查命题的真假判断与应用,考查了空间中直线与平面的位置关系,训练了等积法求棱锥的体积,考查了线面角的求法,是中档题.

练习册系列答案
相关题目
对于R上可导的任意函数f(x),若满足(2-x)f′(x)≤0,则必有( )
| A、f(1)+f(3)<2f(2) |
| B、f(1)+f(3)≤2f(2) |
| C、f(1)+f(3)>2f(2) |
| D、f(1)+f(3)≥2f(2) |
执行如图所示的程序框图,则输出结果S的值为( )


A、
| ||
| B、0 | ||
C、-
| ||
| D、-1 |
 已知a为执行如图所示的程序框图输出的结果,又在数列{an}中,a1=1,an+1=2an+a,则( )
已知a为执行如图所示的程序框图输出的结果,又在数列{an}中,a1=1,an+1=2an+a,则( )A、an=
| ||||
B、an=2n-2+
| ||||
| C、an=3•2n-1-2 | ||||
| D、an=-2n+3 |
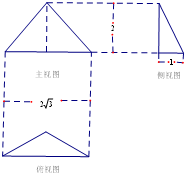
 如图矩形ABCD,AB=4,AD=3,
如图矩形ABCD,AB=4,AD=3,