题目内容
非零向量
,
满足|
|=|
|=
|
+
|,则
与
的夹角大小为 .
| a |
| b |
| a |
| b |
| ||
| 3 |
| a |
| b |
| a |
| b |
考点:数量积表示两个向量的夹角
专题:平面向量及应用
分析:根据条件求出
•
,然后利用数量积的应用即可得到结论.
| a |
| b |
解答:
解:∵|
|=|
|=
|
+
|,
∴平方得
2=
(
2+2
•
+
),
即
•
=
,
∴cos<
,
>=
=
=
,
则<
,
>=60°,
故答案为:60°
| a |
| b |
| ||
| 3 |
| a |
| b |
∴平方得
| a |
| 1 |
| 3 |
| a |
| a |
| b |
| b2 |
即
| a |
| b |
| 1 |
| 2 |
| a2 |
∴cos<
| a |
| b |
| ||||
|
|
| ||||
|
|
| 1 |
| 2 |
则<
| a |
| b |
故答案为:60°
点评:本题主要考查向量夹角的计算,利用向量的数量积是解决本题的关键.

练习册系列答案
相关题目
设A是整数集的一个非空子集,对于k∈A,如果k-1∉A且k+1∉A,那么称k是A的一个“孤立元”,给定S={1,2,3,4,5,6,7,8},则S的3个元素构成的所有集合中,其元素都是“孤立元”的集合个数是( )
| A、6 | B、15 | C、20 | D、25 |
已知集合M是满足下列性质的函数f(x)的集合:存在非零常数k,对定义域中的任意x,等式f(kx)=
+f(x)恒成立.现有两个函数:f(x)=ax+b(a≠0),g(x)=log2x,则函数f(x)、g(x)与集合M的关系为( )
| k |
| 2 |
| A、f(x)∈M,g(x)∈M |
| B、f(x)∉M,g(x)∈M |
| C、f(x)∈M,g(x)∉M |
| D、f(x)∉M,g(x)∉M |
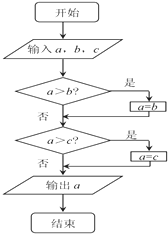
 一个算法的程序框图如图所示,若该程序输出的结果为12,则判断框中应填入的条件是( )
一个算法的程序框图如图所示,若该程序输出的结果为12,则判断框中应填入的条件是( )| A、k≤4 | B、k≤3 |
| C、k<3 | D、k≥3 |
 在[-2,2]上任取一个数,代入三个函数f1(x)=x,f2(x)=x2,f3(x)=x
在[-2,2]上任取一个数,代入三个函数f1(x)=x,f2(x)=x2,f3(x)=x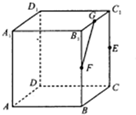 如图,正方体ABCD-A1B1C1D1的棱长为1,E、F、G分别是棱CC1、BB1、B1C1的中点,H是线段FG上一动点,则下列命题正确的是
如图,正方体ABCD-A1B1C1D1的棱长为1,E、F、G分别是棱CC1、BB1、B1C1的中点,H是线段FG上一动点,则下列命题正确的是