题目内容
对于R上可导的任意函数f(x),若满足(2-x)f′(x)≤0,则必有( )
| A、f(1)+f(3)<2f(2) |
| B、f(1)+f(3)≤2f(2) |
| C、f(1)+f(3)>2f(2) |
| D、f(1)+f(3)≥2f(2) |
考点:利用导数研究函数的单调性
专题:导数的概念及应用
分析:由条件分别讨论x>2,x<2时,f'(x)的符号,从而判断f(x)的单调性,求出极值,最值,进而判断f(1)+f(3)与2f(2)的关系.
解答:
解:∵对于R上可导的任意函数f(x),满足(2-x)f′(x)≤0,
①当(2-x)f′(x)<0时,
∴当x<2时,即2-x>0,f'(x)<0,则函数f(x)在(-∞,2)上单调递减,
当x>2,即2-x<0时,f'(x)>0,则函数f(x)在(2,+∞)上单调递增,
∴函数f(x)在x=2处取极小值,又x∈R,则f(2)也是最小值,
∴f(1)>f(2),且f(3)>f(2),
两式相加得:f(1)+f(3)>2f(2).
②当(2-x)f′(x)=0时,即f′(x)=0,
此时有f(x)=f(2),有f(1)+f(3)=2f(2),
综合可得f(1)+f(3)≥2f(2).
故选:D.
①当(2-x)f′(x)<0时,
∴当x<2时,即2-x>0,f'(x)<0,则函数f(x)在(-∞,2)上单调递减,
当x>2,即2-x<0时,f'(x)>0,则函数f(x)在(2,+∞)上单调递增,
∴函数f(x)在x=2处取极小值,又x∈R,则f(2)也是最小值,
∴f(1)>f(2),且f(3)>f(2),
两式相加得:f(1)+f(3)>2f(2).
②当(2-x)f′(x)=0时,即f′(x)=0,
此时有f(x)=f(2),有f(1)+f(3)=2f(2),
综合可得f(1)+f(3)≥2f(2).
故选:D.
点评:本题主要考查运用导数研究函数的单调性,如何求极值、最值,注意开区间内极值只有一个,此时也是最值,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设A是整数集的一个非空子集,对于k∈A,如果k-1∉A且k+1∉A,那么称k是A的一个“孤立元”,给定S={1,2,3,4,5,6,7,8},则S的3个元素构成的所有集合中,其元素都是“孤立元”的集合个数是( )
| A、6 | B、15 | C、20 | D、25 |
已知等差数列{an}的公差d≠0,a1=1且a1,a3,a13成等比数列,若Sn是数列{an}的前n项和,则
的最小值为( )
| 2Sn+14 |
| an+3 |
| A、4 | ||
| B、3 | ||
C、4
| ||
D、
|
已知集合M是满足下列性质的函数f(x)的集合:存在非零常数k,对定义域中的任意x,等式f(kx)=
+f(x)恒成立.现有两个函数:f(x)=ax+b(a≠0),g(x)=log2x,则函数f(x)、g(x)与集合M的关系为( )
| k |
| 2 |
| A、f(x)∈M,g(x)∈M |
| B、f(x)∉M,g(x)∈M |
| C、f(x)∈M,g(x)∉M |
| D、f(x)∉M,g(x)∉M |
已知命题p:?x∈R,cosx=
,命题q:?x∈R,x2-2x+2>0,则下列判断正确的是( )
| 5 |
| 4 |
| A、p∨q为假 |
| B、p∧q为真 |
| C、¬p∨¬q为假 |
| D、¬p∧q为真 |
下列函数中,既是偶函数且值域为(-∞,0]的函数是( )
| A、f(x)=xsinx |
| B、f(x)=-2-x |
| C、f(x)=ln|x| |
| D、f(x)=-x2 |
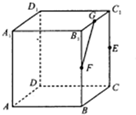 如图,正方体ABCD-A1B1C1D1的棱长为1,E、F、G分别是棱CC1、BB1、B1C1的中点,H是线段FG上一动点,则下列命题正确的是
如图,正方体ABCD-A1B1C1D1的棱长为1,E、F、G分别是棱CC1、BB1、B1C1的中点,H是线段FG上一动点,则下列命题正确的是