题目内容
 如图矩形ABCD,AB=4,AD=3,
如图矩形ABCD,AB=4,AD=3,| AE |
| 1 |
| 4 |
| AB |
考点:几何概型
专题:概率与统计
分析:建立坐标系,利用向量数量积的应用,建立条件关系,利用几何槪型的概率公式即可得到结论.
解答:
解:设FA=y,GD=x,以A为坐标原点,建立直角坐标系如图:则0≤y≤3,0≤x≤4,平面区域{(x,y)|0≤y≤3,0≤x≤4}对应的区域是长方形,
面积S=12.
则F(0,y),E(1,0),G(3,x),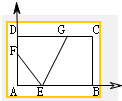
则
=(-1,y),
=(2,x),
若∠FEG是锐角,则
•
=-2+xy>0,
即xy>2,y>
,(0≤x≤4),
作出对应的平面区域如图:
当y=3时,由
=3,解得x=
,P(
,3),
阴影部分的面积S=
(3-
)dx=(3x-2lnx)|
=10-2ln6,
∴根据几何概型的概率公式可得∠FEG为锐角的概率
=
,
故答案为:
面积S=12.
则F(0,y),E(1,0),G(3,x),

则
| EF |
| EG |
若∠FEG是锐角,则
| EF |
| EG |
即xy>2,y>
| 2 |
| x |
作出对应的平面区域如图:
当y=3时,由
| 2 |
| x |
| 2 |
| 3 |
| 2 |
| 3 |

阴影部分的面积S=
| ∫ | 4
|
| 2 |
| x |
4
|
∴根据几何概型的概率公式可得∠FEG为锐角的概率
| 10-2ln6 |
| 12 |
| 5-ln6 |
| 6 |
故答案为:
| 5-ln6 |
| 6 |
点评:本题主要考查几何概型的概率计算,利用数量积的应用,结合积分求出对应区域的面积是解决本题的关键,综合性较强,涉及的知识点较多.

练习册系列答案
相关题目
执行如图所示的程序框图,则输出的S的值为( )


| A、-7 | B、8 | C、-9 | D、-5 |
已知等差数列{an}的公差d≠0,a1=1且a1,a3,a13成等比数列,若Sn是数列{an}的前n项和,则
的最小值为( )
| 2Sn+14 |
| an+3 |
| A、4 | ||
| B、3 | ||
C、4
| ||
D、
|
已知集合M=(-2,-1,0,1,2,3},N={x|y=
},则M∩N为( )
| ln(3-x) | ||
|
| A、{0,1,2} |
| B、{-1,0,1,2} |
| C、{-2,-1,0} |
| D、{0,1,2,3} |
函数f(x)=sin(ωx+
)(ω>0)的图象与x轴的交点的横坐标构成一个公差为
的等差数列,要得到函数g(x)=sinωx的图象,只需将f(x)的图象( )
| π |
| 6 |
| π |
| 2 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|

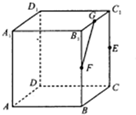 如图,正方体ABCD-A1B1C1D1的棱长为1,E、F、G分别是棱CC1、BB1、B1C1的中点,H是线段FG上一动点,则下列命题正确的是
如图,正方体ABCD-A1B1C1D1的棱长为1,E、F、G分别是棱CC1、BB1、B1C1的中点,H是线段FG上一动点,则下列命题正确的是