题目内容
已知二次函数f(x)=ax2+bx+c(a,b,c∈R)满足f(-1)=0,f(1)=1,且对任意实数x都有f(x)-x≥0,求f(x)的解析式.
考点:二次函数的性质
专题:函数的性质及应用
分析:由已知条件,可得
,解方程组求出a,b,c的值,代入可求出f(x)的解析式.
|
解答:
解:∵二次函数f(x)=ax2+bx+c(a,b,c∈R)满足f(-1)=0,f(1)=1,
且对任意实数x都有f(x)-x≥0,
而f(1)=1,即f(1)-1=0,方程f(x)-x=0有解x=1,
则必有(b-1)2-4ac≥0,
∴
即
,当a=c=
时,ac=
,
此时
∴f(x)=
x2+
x+
.
且对任意实数x都有f(x)-x≥0,
而f(1)=1,即f(1)-1=0,方程f(x)-x=0有解x=1,
则必有(b-1)2-4ac≥0,
∴
|
即
|
| 1 |
| 4 |
| 1 |
| 16 |
此时
|
∴f(x)=
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
点评:本题考查的知识点是二次函数的性质,二次函数解析式的求法,其中根据已知构造方程组
是解答的关键.
|

练习册系列答案
相关题目
抛物线y=x2-4x-4的顶点坐标是( )
| A、(2,0) |
| B、(2,-2) |
| C、(2,-8) |
| D、(-2,-8) |
从1、2、3、4这四个数中一次随机取两个,则取出的这两数字之和为偶数的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
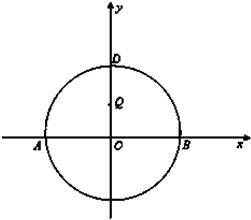 如图,AB为圆O直径,已知A(-2,0)、B(2,0),D为圆O上的一点,且
如图,AB为圆O直径,已知A(-2,0)、B(2,0),D为圆O上的一点,且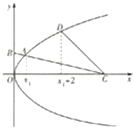 抛物线M:y2=2px(p>0)的准线过椭圆N:
抛物线M:y2=2px(p>0)的准线过椭圆N: