题目内容
抛物线y=x2-4x-4的顶点坐标是( )
| A、(2,0) |
| B、(2,-2) |
| C、(2,-8) |
| D、(-2,-8) |
考点:二次函数的性质
专题:函数的性质及应用
分析:可直接利用顶点公式可求顶点坐标.也可以用配方法求解.
解答:
解法1:利用公式法:
y=ax2+bx+c的顶点坐标公式为(-
,
),
∴二次函数y=x2-4x-4图象的顶点坐标为(2,-8),
故选:C.
解法2:利用配方法:
y=x2-4x-4=(x2-4x+4)-8=(x-2)2-8,
∴二次函数y=x2-4x-4图象的顶点坐标为(2,-8),
故选:C.
y=ax2+bx+c的顶点坐标公式为(-
| b |
| 2a |
| 4ac-b2 |
| 4a |
∴二次函数y=x2-4x-4图象的顶点坐标为(2,-8),
故选:C.
解法2:利用配方法:
y=x2-4x-4=(x2-4x+4)-8=(x-2)2-8,
∴二次函数y=x2-4x-4图象的顶点坐标为(2,-8),
故选:C.
点评:本题考查的知识点是二次函数的图象和性质,是对二次函数基本知识点的考查,难度不大,属于基础题.

练习册系列答案
相关题目
如图所示的程序框图,如果输入m=225,n=135,那么输出的值为( )


| A、45 | B、5 | C、15 | D、90 |
已知复数z1=2+i,z2=a-i,z1•z2是实数,则实数a=( )
| A、2 | B、3 | C、4 | D、5 |
已知某空间几何体的三视图(单位:cm)如图所示,则该几何体的体积是( )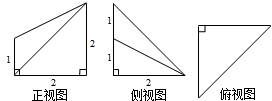

| A、2cm3 | ||
B、
| ||
| C、1cm3 | ||
| D、6cm3 |
设双曲线C:
-
=1(a>0)的一个顶点坐标为(2,0),则双曲线C的方程是( )
| x2 |
| a2 |
| y2 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|