Question

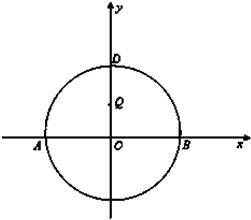如图，AB为圆O直径，已知A（-2，0）、B（2，0），D为圆O上的一点，且O

A

•O

D

=0，Q为线段OD的中点，曲线C过Q点，动点G在曲线C上运动且保持|GA|+|GB|的值不变
（Ⅰ）求曲线C的方程；
（Ⅱ）过点D的直线l与曲线C相交于不同的两点M、N，且M在D、N之间，设

DM

DN

=λ，求λ的取值范．

Answer 1

考点：直线与圆锥曲线的综合问题

专题：圆锥曲线的定义、性质与方程

分析：（Ⅰ）由题意可知，曲线C为以原点为中心，A、B为焦点的椭圆，结合已知条件求出椭圆的长半轴长和短半轴长，则椭圆方程可求；
（Ⅱ）分直线l的斜率存在和不存在两种情况讨论，斜率不存在时直接求得λ的值，斜率存在时设出直线l的方程，和（Ⅰ）中求得的方程联立后由判别式大于0得到斜率的范围，再由根与系数关系结合

DM

DN

=

x1

x2

=λ (λ＞0)整体化简得到

(1+λ)2

λ

=

80

3(5+ 1 k2 )

，由判别式中求得的k的范围代入求得λ的范围．

解答： 解：（Ⅰ）如图，

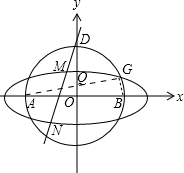
∵|GA|+|GB|=|QA|+|QB|=2

5

＞|AB|
∴曲线C为以原点为中心，A、B为焦点的椭圆
设其长半轴为a，短半轴为b，半焦距为c，
则a=

5

，c=2，b=1，
∴曲线C的方程为

x2

5

+y2=1；
（Ⅱ）当k不存在时，显然λ=

DM

DN

=

1

3

（此时直线l与y轴重合），
当k存在时，设直线l的方程为y=kx+2，代入

x2

5

+y2=1，得（1+5k²）x²+20kx+15=0．
△=（20k）²-4×15（1+5k²）＞0，得k2＞

3

5

．
设M（x₁，y₁），N（x₂，y₂），
则

DM

DN

=

x1

x2

=λ (λ＞0)，
由根与系数关系得

x1+x2=- 20k 1+5k2 x1x2= 15 1+5k2

，将x₁=λx₂代入得，

(1+λ)2x22= 400k2 (1+5k2)2 λx22= 15 1+5k2

，∴

(1+λ)2

λ

=

400k2

15(1+5k2)

=

80

3(5+ 1 k2 )

．
∵k2＞

3

5

，
∴4＜

80

3( 1 k2 +5)

＜

16

3

，
∴4＜

(1+λ)2

λ

＜

16

3

，
∵λ=

DM

DN

＞0，解得

1

3

＜λ＜3 ①
又∵M在D、N之间，
∴λ=

DM

DN

＜1 ②
综①②可得

1

3

≤λ＜1．

点评：本题主要椭圆方程的求法，考查了直线与椭圆的位置关系的应用，直线与曲线联立，根据方程的根与系数的关系解题，是处理这类问题的最为常用的方法，但圆锥曲线的特点是计算量比较大，要求考试具备较强的运算推理的能力，是高考试卷中的压轴题．