Question

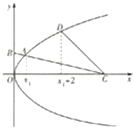抛物线M：y²=2px（p＞0）的准线过椭圆N：

4x2

5

+y²=1的左焦点，以坐标原点为圆心，以t（t＞0）为半径的圆分别与抛物线M在第一象限的部分以及y轴的正半轴相交于点A与点B，直线AB与x轴相交于点C．
（1）求抛物线M的方程；
（2）设点A的横坐标为x₁，点C的横坐标为x₂，曲线M上点D的横坐标为x₁+2，求直线CD的斜率．

Answer 1

考点：直线与圆锥曲线的综合问题

专题：圆锥曲线的定义、性质与方程

分析：（1）由椭圆方程求出椭圆左焦点坐标，得到抛物线焦点坐标，从而求得p值，则抛物线方程可求；
（2）写出A的坐标，由|OA|=t列式求得t与A的坐标间的关系，求出直线BC的方程，把A代入BC方程，得到
x₁，x₂ 的关系，然后直接代入斜率公式求直线CD的斜率．

解答： 解：（1）∵椭圆N：

4x2

5

+y²=1，
∴c2=a2-b2=

5

4

-1=

1

4

，
∴椭圆的左焦点为F1(-

1

2

，0)，
∴-

p

2

=-

1

2

，则p=1．
故M：y²=2x；
（2）由题意知，A(x1，

2x1

)，
∵|OA|=t，
∴x12+2x1=t2．
由于t＞0，故有t=

x12+2x1

  ①
由点B（0，t），C（x₂，0）的坐标知，
直线BC的方程为

x

x2

+

y

t

=1．
又∵A在直线BC上，故有

x1

x2

+

2x1

t

=1．
将①代入上式，得     

x1

x2

+

2x1

x1(x1+2)

=1，解得x2=x1+2+

2(x1+2)

．
又∵D（x₁+2，2

2(x1+2)

），
∴直线CD的斜率为：
kCD=

2(x1+2)

x1+2-x2

=

2(x1+2)

x1+2-(x1+2+ 2(x1+2) )

=

2(x1+2)

- 2(x1+2)

=-1．

点评：本题主要抛物线方程的求法，考查了直线与圆锥曲线位置关系的应用，解答此题的关键是对抛物线定义的灵活应用，是高考试卷中的压轴题．