题目内容
从1、2、3、4这四个数中一次随机取两个,则取出的这两数字之和为偶数的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:古典概型及其概率计算公式
专题:概率与统计
分析:根据古典概型的概率公式分别进行计算即可得到结论.
解答:
解:从1、2、3、4这四个数中一次随机取两个,共有
=6种结果,
满足取出的这两数字之和为偶数的有2和4,以及1和3,共2种,
则根据古典概型的概率公式可知取出的这两数字之和为偶数的概率P=
=
,
故选:B.
| C | 2 4 |
满足取出的这两数字之和为偶数的有2和4,以及1和3,共2种,
则根据古典概型的概率公式可知取出的这两数字之和为偶数的概率P=
| 2 |
| 6 |
| 1 |
| 3 |
故选:B.
点评:本题主要考查古典概型的概率计算,根据条件分别求出基本事件的个数是解决本题的关键,比较基础.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
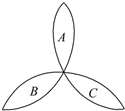 荷花池中,有一只青蛙在成品字形的三片荷叶上跳来跳去(每次跳跃时,均从一叶跳到另一叶),而且逆时针方向跳的概率是顺时针方向跳的概率的两倍,如图所示.假设现在青蛙在A叶上,则跳四次之后停在A叶上的概率是( )
荷花池中,有一只青蛙在成品字形的三片荷叶上跳来跳去(每次跳跃时,均从一叶跳到另一叶),而且逆时针方向跳的概率是顺时针方向跳的概率的两倍,如图所示.假设现在青蛙在A叶上,则跳四次之后停在A叶上的概率是( )A、
| ||
B、
| ||
C、
| ||
D、
|
已知圆C的圆心是直线x-y+1=0与x轴的交点,且圆C与直线x+y+3=0相切,则圆C的方程是( )
| A、(x+1)2+y2=2 |
| B、(x+1)2+y2=8 |
| C、(x-1)2+y2=2 |
| D、(x-1)2+y2=8 |
给出程序框图,若输入的x值为-5,则输出的y的值是( )


| A、-2 | B、-1 | C、0 | D、1 |