题目内容
当x∈[-1,2]时,函数f(x)=-x2-ax+b的图象恒在x轴的上方,则
的取值范围是多少?
| b |
| a |
考点:二次函数的性质
专题:函数的性质及应用
分析:根据已知结合二次函数的图象和性质,可得
,进而构造关于a,b的二元一次不等式组,将问题转化为线性规划问题,进而结合
的几何意义得到答案.
|
| b |
| a |
解答:
解:∵函数f(x)=-x2-ax+b的图象开口方向朝下,
且当x∈[-1,2]时,函数f(x)=-x2-ax+b的图象恒在x轴的上方,
故
,
即
,
其对应的平面区域如下图所示:
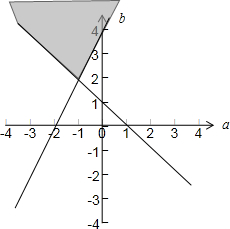
表示平面区域内动点(a,b)与原点连线的斜率,
故
的范围为(-∞,-1)∪(2,+∞)
且当x∈[-1,2]时,函数f(x)=-x2-ax+b的图象恒在x轴的上方,
故
|
即
|
其对应的平面区域如下图所示:

| b |
| a |
故
| b |
| a |
点评:本题考查的知识点是二次函数的性质,线性规划,分式的几何意义,是函数、不等式、解析几何的综合应用,难度中档.

练习册系列答案
相关题目
已知某空间几何体的三视图(单位:cm)如图所示,则该几何体的体积是( )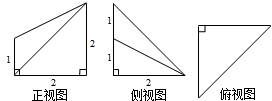

| A、2cm3 | ||
B、
| ||
| C、1cm3 | ||
| D、6cm3 |
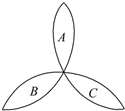 荷花池中,有一只青蛙在成品字形的三片荷叶上跳来跳去(每次跳跃时,均从一叶跳到另一叶),而且逆时针方向跳的概率是顺时针方向跳的概率的两倍,如图所示.假设现在青蛙在A叶上,则跳四次之后停在A叶上的概率是( )
荷花池中,有一只青蛙在成品字形的三片荷叶上跳来跳去(每次跳跃时,均从一叶跳到另一叶),而且逆时针方向跳的概率是顺时针方向跳的概率的两倍,如图所示.假设现在青蛙在A叶上,则跳四次之后停在A叶上的概率是( )