题目内容

2，8的等比中项为
 
．
考点：等比数列的通项公式
专题：等差数列与等比数列
分析：直接由等比中项的概念得答案．
解答： 解：设2，8的等比中项为m，
则m2=2×8=16，
∴m=±4．
故答案为：±4．
点评：本题考查了等比中项的概念，是基础的会考题型．
练习册系列答案
相关题目
首项为20的等差数列{an}，前n项和Sn且S11＜0＜S10，则公差d的范围
 
．
已知函数f（x）=x3+x（x≥0），对于曲线y=f（x）上横坐标成公差为1的等差数列的三个点A，B，C，给出以下判断：其中所有正确的序号是
 
．
①△ABC一定是钝角三角形；
②△ABC可能是直角三角形；
③△ABC可能是等腰三角形；
④△ABC不可能是等腰三角形．
函数f（x）=
2-
x+3
x+1
的定义域为
 
．
在平面直角坐标系中，定义d（A，B）=|x1-x2|+|y1-y2|为两点A（x1，x2），B（y1，y2）的“直角距离”，已知直线l经过点P（
5
，0），倾斜角为α，且cosα=-
5
5
，在直线l上截取线段EF（-
5
≤x≤2
5
），则原点O与线段EF上一点的“直角距离”的最小值与最大值之和是
 
．
已知f（x）=kx+b（k＜0），且f[f（x）]=4x+1，则f（x）=（　　）
A、-2x-1
B、-2x+1
C、-x+1
D、-2x-
1
2
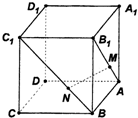如图所示，在正方体ABCD-A1B1C1D1中，点M、N分别在线段AB1、BC1上，且AM=BN．给出下列结论：
①MN与A1C1相交；
②MN∥A1C1；
③MN与A1C1异面，
其中有可能成立的结论的个数为（　　）
A、3B、2C、1D、0
设集合U=﹛1，2，3，4﹜，A=﹛1，2﹜，B=﹛2，4﹜，则∁U（A∪B）=（　　）
A、﹛2﹜B、﹛3﹜
C、﹛1，4﹜D、﹛1，3，4﹜
在Rt△ABC中，∠CAB=90°，AB=2，AC=
2
2
，一曲线E过C点，动点P在曲线E上运动，且保持|PA|+|PB|的值不变．直线m⊥AB于O，AO=BO．
（1）建立适当的坐标系，求曲线E的方程；
（2）设D为直线m上一点，
OD
=
AC
，过点D引直线l交曲线E于M、N两点，保持直线l与AB成45°，求四边形MANB的面积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网