题目内容
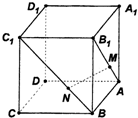如图所示，在正方体ABCD-A1B1C1D1中，点M、N分别在线段AB1、BC1上，且AM=BN．给出下列结论：①MN与A1C1相交；
②MN∥A1C1；
③MN与A1C1异面，
其中有可能成立的结论的个数为（ ）
| A、3 | B、2 | C、1 | D、0 |
考点：空间中直线与平面之间的位置关系
专题：空间位置关系与距离
分析：作NE⊥BC，MF⊥AB，则四边形MNEF是矩形，MN∥FE，由FE与AC所在直线相交，得MN与A1C1异面．
解答：
解：作NE⊥BC，MF⊥AB，垂足分别为E，F，
由已知得四边形MNEF是矩形，
∴MN∥FE，
∵FE与AC所在直线相交，
∴MN与A1C1异面．
故①②均错误，③正确．
故选：C．
由已知得四边形MNEF是矩形，
∴MN∥FE，
∵FE与AC所在直线相交，
∴MN与A1C1异面．
故①②均错误，③正确．
故选：C．
点评：本题考查命题真假的判断，是基础题，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
阅读快车系列答案
相关题目
不等式x2-2x-15≤0的解集为（ ）
| A、[-5，3] |
| B、[-3，5] |
| C、（-∞，-3]∪[5，+∞） |
| D、（-∞，-5]∪[3，+∞） |
已知
是非零向量，
≠
，则“
•
=
•
”是“
⊥(
-
)”成立的（ ）
| a |
| b |
| c |
| a |
| b |
| a |
| c |
| a |
| b |
| c |
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、非充分非必要条件 |
| D、充要条件 |
若sin（π+α）=
，α是第三象限的角，则
=（ ）
| 3 |
| 5 |
sin
| ||||
sin
|
A、
| ||
B、-
| ||
| C、2 | ||
| D、-2 |
