题目内容
(1)设正实数x,y满足条件
,则2lgx+lgy的最大值为
(2)设P,Q分别为圆x2+(y-6)2=2和椭圆
+y2=1上的点,则P,Q两点间的最大距离是 .
|
(2)设P,Q分别为圆x2+(y-6)2=2和椭圆
| x2 |
| 10 |
考点:简单线性规划,对数的运算性质,椭圆的简单性质
专题:不等式的解法及应用
分析:(1)设a=lgx,b=lgy,将不等式组进行转化,利用线性规划的知识进行求解.
(2)求出椭圆上的点与圆心的最大距离,加上半径,即可得出P,Q两点间的最大距离.
(2)求出椭圆上的点与圆心的最大距离,加上半径,即可得出P,Q两点间的最大距离.
解答:
解:(1)设a=lgx,b=lgy,则不等式等价为
,目标函数z=2a+b,
即b=-2a+z,
作出不等式组对应的平面区域如图:
平移直线b=-2a+z,当直线b=-2a+z经过点A(1,0)时,直线的截距最大,此时z最大,为z=2+0=2,
即2lgx+lgy的最大值为2.
(2)设椭圆上的点为(x,y),则x2=10-10y2,
∵圆x2+(y-6)2=2的圆心为(0,6),半径为
,
∴椭圆上的点与圆心的距离为
=
=
≤5
,
∴P,Q两点间的最大距离是5
+
=6
.
故答案为:(1)2; (2)6
;
|
即b=-2a+z,

作出不等式组对应的平面区域如图:
平移直线b=-2a+z,当直线b=-2a+z经过点A(1,0)时,直线的截距最大,此时z最大,为z=2+0=2,
即2lgx+lgy的最大值为2.
(2)设椭圆上的点为(x,y),则x2=10-10y2,
∵圆x2+(y-6)2=2的圆心为(0,6),半径为
| 2 |
∴椭圆上的点与圆心的距离为
| x2+(y-6)2 |
| 10-10y2+(y-6)2 |
-9(y+
|
| 2 |
∴P,Q两点间的最大距离是5
| 2 |
| 2 |
| 2 |
故答案为:(1)2; (2)6
| 2 |
点评:本题主要考查线性规划的应用,利用目标函数的几何意义,结合数形结合的数学思想是解决此类问题的基本方法.

练习册系列答案
相关题目
若点P到直线y=-2的距离比它到点A(0,1)的距离大1,则点P的轨迹为( )
| A、圆 | B、椭圆 | C、双曲线 | D、抛物线 |
若k∈[-3,3],则k的值使得过A(1,1)可以做两条直线与圆(x-k)2+y2=2相切的概率等于( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知点P的横坐标为2,以P为圆心的圆交x轴于A、B两点,若直线AP的方程为x-y+1=0,则直线BP的方程为( )
| A、x-y-5=0 |
| B、x+y-5=0 |
| C、2x+y-5=0 |
| D、2x-y+5=0 |
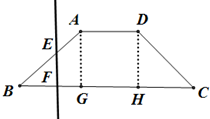 如图,已知底角为45°的等腰梯形ABCD,底边BC长为5cm,腰长为2
如图,已知底角为45°的等腰梯形ABCD,底边BC长为5cm,腰长为2