Question

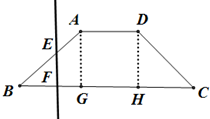如图，已知底角为45°的等腰梯形ABCD，底边BC长为5cm，腰长为2

2

cm，当一条垂直于底边BC的直线l从左至右移动（与梯形ABCD有公共点）时，直线l把梯形分成两部分，令BF=x，试写出左边部分的面积y与x的函数解析式，并画出大致图象．

Answer 1

考点：函数的图象

专题：函数的性质及应用

分析：过A，D分别作AG⊥BC于G，DH⊥BC于H，由平面图形的知识可得线段长度，由面积公式分段可得函数解析式，作图可得．

解答： 解：过A，D分别作AG⊥BC于G，DH⊥BC于H，
∵ABCD是等腰梯形，底角45°，AB=2

2

cm，
∴BG=AG=DH=HC=2cm，又BC=5cm，∴AD=GH=1cm，
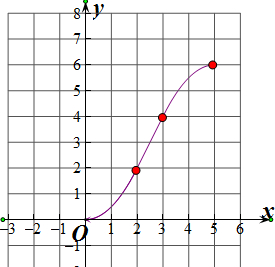
（1）当点F在BG上，即x∈[0，2]时，y=

1

2

x²，
（2）当点F在GH上，即x∈（2，3]时，
y=2+2（x-2）=2x-2，
（3）当点F在HC上，即x∈（3，5]时，y=-

1

2

（x-5）²+6，
∴函数的解析式为y=

1 2 x2，x∈[0，2] 2x-2，x∈(2，3] - 1 2 (x-5)2+6，x∈(3，5]

作图如右：

点评：本题考查求分段函数的解析式，找到分段点，在各段找出已学过得的规则图形，化未知为已知，结合图形，比较直观．用到转化，化归与数形结合的思想．