题目内容
已知a∈R,f(x)=x2+3x-a2-3a
(1)当a=4时,求不等式f(x)>0;
(2)设A=[-8,-4],不等式f(x)>0的解集为B,如果A⊆B,求实数a的取值范围.
(1)当a=4时,求不等式f(x)>0;
(2)设A=[-8,-4],不等式f(x)>0的解集为B,如果A⊆B,求实数a的取值范围.
考点:二次函数的性质
专题:函数的性质及应用
分析:(1)将a=4代入后,构造关于x的二次不等式,解不等式可得答案;
(2)不等式f(x)>0的解集为B=(-∞,-a-3)∪(a,+∞),或B=(-∞,a∪(-a-3,+∞),根据A⊆B,构造关于a的不等式,解不等式可得答案.
(2)不等式f(x)>0的解集为B=(-∞,-a-3)∪(a,+∞),或B=(-∞,a∪(-a-3,+∞),根据A⊆B,构造关于a的不等式,解不等式可得答案.
解答:
解:(1)当a=4时,f(x)=x2+3x-28,
则不等式f(x)>0可化为x2+3x-28>0,
即(x+7)(x-4)>0,
解得x<-7,或x>4,
故不等式f(x)>0的解集为(-∞,-7)∪(4,+∞);
(2)∵f(x)=x2+3x-a2-3a=(x+a+3)(x-a)
当-a-3≤a,即a≥-
时,不等式f(x)>0的解集为B=(-∞,-a-3)∪(a,+∞),
若A⊆B,则-4<-a-3或-8>a,
∴-
≤a<1
当-a-3>a,即a<-
时,不等式f(x)>0的解集为B=(-∞,a∪(-a-3,+∞),
若A⊆B,则-4<a或-8>-a-3,
∴-4<a<-
综上实数a的取值范围-4<a<1
则不等式f(x)>0可化为x2+3x-28>0,
即(x+7)(x-4)>0,
解得x<-7,或x>4,
故不等式f(x)>0的解集为(-∞,-7)∪(4,+∞);
(2)∵f(x)=x2+3x-a2-3a=(x+a+3)(x-a)
当-a-3≤a,即a≥-
| 3 |
| 2 |
若A⊆B,则-4<-a-3或-8>a,
∴-
| 3 |
| 2 |
当-a-3>a,即a<-
| 3 |
| 2 |
若A⊆B,则-4<a或-8>-a-3,
∴-4<a<-
| 3 |
| 2 |
综上实数a的取值范围-4<a<1
点评:本题考查的知识点是二次函数的性质,解二次不等式,是函数与不等式的综合应用,难度中档.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
如图所示的程序框图,能使输入的x值与输出的y值相等的所有x值分别为( )


| A、1、2、3 |
| B、0、1 |
| C、0、1、3 |
| D、0、1、2、3、4 |
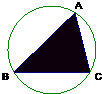 如图已知圆的半径为10,其内接三角形ABC的内角A、B分别为60°和45°,现向圆内随机撒一粒豆子,则豆子落在三角形ABC内的概率为( )
如图已知圆的半径为10,其内接三角形ABC的内角A、B分别为60°和45°,现向圆内随机撒一粒豆子,则豆子落在三角形ABC内的概率为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 甲、乙两家商场对同一种商品开展促销活动,对购买该商品的顾客两家商场的奖励方案如下:
甲、乙两家商场对同一种商品开展促销活动,对购买该商品的顾客两家商场的奖励方案如下: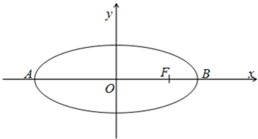 在平面直角坐标系xoy中,如图,已知椭圆
在平面直角坐标系xoy中,如图,已知椭圆