题目内容
甲、乙、丙三个车床加工的零件分别为350个,700个,1050个,现用分层抽样的方法随机抽取6个零件进行检验.
(Ⅰ)从抽取的6个零件中任意取出2个,已知这两个零件都不是甲车床加工的,求至少有一个是乙车床加工的概率;
(Ⅱ)从抽取的6个零件中任意取出3个,记其中是乙车床加工的件数为X,求X的分布列和期望.
(Ⅰ)从抽取的6个零件中任意取出2个,已知这两个零件都不是甲车床加工的,求至少有一个是乙车床加工的概率;
(Ⅱ)从抽取的6个零件中任意取出3个,记其中是乙车床加工的件数为X,求X的分布列和期望.
考点:离散型随机变量的期望与方差,互斥事件与对立事件
专题:计算题,概率与统计
分析:(Ⅰ)根据分层抽样的定义即可求出求从甲、乙、丙三个车床中抽取的零件的件数,根据古典概率的概率公式即可求出相应的概率公式;
(Ⅱ)X的可能取值为0,1,2,则P(X=i)=
(i=0,1,2),可得X的分布列,即可求出X的期望.
(Ⅱ)X的可能取值为0,1,2,则P(X=i)=
| ||||
|
解答:
解:(Ⅰ)由抽样方法可知,从甲、乙、丙三个车床抽取的零件数分别为1,2,3.
设从抽取的6个零件为a1,b1,b2,c1,c2,c3.
事件“已知这两个零件都不是甲车床加工的”的可能结果为(b1,b2),(b1,c1),(b1,c2),(b1,c3),(b2,c1),(b2,c2),(b2,c3),(c1,c2),(c1,c3),(c2,c3),共10种可能;
事件“其中至少有一个是乙车床加工的”的可能结果为(b1,b2),(b1,c1),(b1,c2),(b1,c3),(b2,c1),(b2,c2),(b2,c3),共7种可能.
故所求概率为P=0.7;
(Ⅱ)X的可能取值为0,1,2,则P(X=i)=
(i=0,1,2)
X的分布列为
X的期望为E(X)=0×0.2+1×0.6+2×0.2=1
设从抽取的6个零件为a1,b1,b2,c1,c2,c3.
事件“已知这两个零件都不是甲车床加工的”的可能结果为(b1,b2),(b1,c1),(b1,c2),(b1,c3),(b2,c1),(b2,c2),(b2,c3),(c1,c2),(c1,c3),(c2,c3),共10种可能;
事件“其中至少有一个是乙车床加工的”的可能结果为(b1,b2),(b1,c1),(b1,c2),(b1,c3),(b2,c1),(b2,c2),(b2,c3),共7种可能.
故所求概率为P=0.7;
(Ⅱ)X的可能取值为0,1,2,则P(X=i)=
| ||||
|
X的分布列为
| X | 0 | 1 | 2 |
| P | 0.2 | 0.6 | 0.2 |
点评:本题主要考查了离散型随机变量及其分布列和数学期望,考查分层抽样的定义和应用,以及古典概率的概率公式的计算,要求熟练掌握概率的概率公式.

练习册系列答案
相关题目
已知α∈(
,π),且tan(α+
)=-
,则sinα+cosα的值是( )
| π |
| 2 |
| π |
| 4 |
| 1 |
| 7 |
A、
| ||
B、-
| ||
C、-
| ||
D、-
|
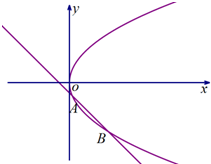 已知抛物线C:y2=4x,直线l:y=-x+b与抛物线C交于A,B两点.
已知抛物线C:y2=4x,直线l:y=-x+b与抛物线C交于A,B两点.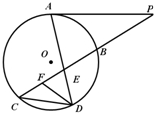 如图所示,已知PA与⊙O相切,A为切点,过点P的割线交圆于B、C两点,弦CD∥AP,AD、BC相交于点E,F为CE上一点,且∠EDF=∠C,若CE:BE=3:2,DE=3,EF=2.则PA=
如图所示,已知PA与⊙O相切,A为切点,过点P的割线交圆于B、C两点,弦CD∥AP,AD、BC相交于点E,F为CE上一点,且∠EDF=∠C,若CE:BE=3:2,DE=3,EF=2.则PA=