题目内容
求函数f(x)=x2-
+2x+1的值域.
| 1 |
| x2 |
考点:函数的值域
专题:函数的性质及应用,导数的概念及应用
分析:先求定义域为(-∞,0)∪(0,+∞),再求导函数f′(x)=2x+2x-3+2,根据导函数判断合适的单调区间,即可得函数值域.
解答:
解:f(x)=x2-
+2x+1,得x∈(-∞,0)∪(0,+∞)
f′(x)=x2+
+2,当x∈(0,+∞)时,f′(x)>0恒成立
∴y=f(x)在x∈(0,+∞)上是单调递增函数,值域为(-∞,+∞)
当x∈(-∞,0)时,无论函数值取什么,都不改变函数值域为(-∞,+∞)
故函数的值域为(-∞,+∞)
| 1 |
| x2 |
f′(x)=x2+
| 2 |
| x3 |
∴y=f(x)在x∈(0,+∞)上是单调递增函数,值域为(-∞,+∞)
当x∈(-∞,0)时,无论函数值取什么,都不改变函数值域为(-∞,+∞)
故函数的值域为(-∞,+∞)
点评:当遇到函数求值域时时,处理的步骤一般为:①根据“让解析式有意义”的原则,先确定函数的定义域;②再根据函数的单调区间求值域;③根据定义域和解析式画出函数的图象;④根据图象分析函数的性质.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
已知x,y满足约束条件
,则z=2x+4y的最小值是( )
|
| A、-6 | B、5 | C、38 | D、-10 |
已知
=(1,2),
=(3,4),则向量
在
方向上的投影为( )
| a |
| b |
| b |
| a |
| A、5 | ||||
B、
| ||||
| C、3 | ||||
D、
|
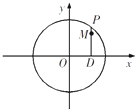 如图,设P是圆x2+y2=25上的动点,点D是P在x轴上的投影,M为PD上一点,且
如图,设P是圆x2+y2=25上的动点,点D是P在x轴上的投影,M为PD上一点,且