题目内容
2．已知向量$\overrightarrow{{e}_{1}}$，$\overrightarrow{{e}_{2}}$，$\overrightarrow{{e}_{3}}$是两两垂直的单位向量，且$\overrightarrow{a}$=3$\overrightarrow{{e}_{1}}$+2$\overrightarrow{{e}_{2}}$-$\overrightarrow{{e}_{3}}$，$\overrightarrow{b}$=$\overrightarrow{{e}_{1}}$+2$\overrightarrow{{e}_{2}}$，则（6$\overrightarrow{a}$）•（$\frac{1}{2}$$\overrightarrow{b}$）等于21．分析 根据单位向量的定义和向量的乘法运算计算即可．
解答 解：$\overrightarrow{a}$=3$\overrightarrow{{e}_{1}}$+2$\overrightarrow{{e}_{2}}$-$\overrightarrow{{e}_{3}}$，$\overrightarrow{b}$=$\overrightarrow{{e}_{1}}$+2$\overrightarrow{{e}_{2}}$，向量$\overrightarrow{{e}_{1}}$，$\overrightarrow{{e}_{2}}$，$\overrightarrow{{e}_{3}}$是两两垂直的单位向量，
则（6$\overrightarrow{a}$）•（$\frac{1}{2}$$\overrightarrow{b}$）=3$\overrightarrow{a}$•$\overrightarrow{b}$=3（3$\overrightarrow{{e}_{1}}$+2$\overrightarrow{{e}_{2}}$-$\overrightarrow{{e}_{3}}$）•（$\overrightarrow{{e}_{1}}$+2$\overrightarrow{{e}_{2}}$）=3（3$\overrightarrow{{e}_{1}}$2+2$\overrightarrow{{e}_{1}}$•$\overrightarrow{{e}_{2}}$-$\overrightarrow{{e}_{1}}$•$\overrightarrow{{e}_{3}}$+6$\overrightarrow{{e}_{1}}$$\overrightarrow{{e}_{2}}$+4$\overrightarrow{{e}_{2}}$2-2$\overrightarrow{{e}_{3}}$•$\overrightarrow{{e}_{2}}$）=3（3+4）=21，
故答案为：21．
点评 本题考查了单位向量和向量的数量积的运算，属于基础题．
导学全程练创优训练系列答案
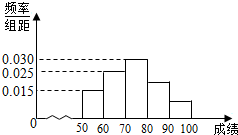某校共有400名学生参加了一次数学竞赛，竞赛成绩都在[50，100]内，且频率分布直方图如图所示（成绩分组为[50，60]，[60，70]，[70，80），[80，90），[90，100]），则在本次竞赛中，得分不低于80分的人数为120．
如图，已知AD是△ABC的外角∠EAC的平分线，交BC的延长线于点D，延长DA交△ABC的外接圆于点F，连接FB，FC．