题目内容
12．
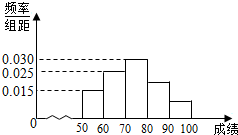某校共有400名学生参加了一次数学竞赛，竞赛成绩都在[50，100]内，且频率分布直方图如图所示（成绩分组为[50，60]，[60，70]，[70，80），[80，90），[90，100]），则在本次竞赛中，得分不低于80分的人数为120．
分析 由频率分布直方图求出得分不低于80分的频率，由此能求出得分不低于80分的人数．
解答 解：由频率分布直方图得：
得分不低于80分的频率为：1-（0.015+0.025+0.030）×10=0.3，
∴得分不低于80分的人数为：400×0.3=120人．
故答案为：120．
点评 本题考查频率分布直方图的应用，是基础题，解题时要认真审题，注意频率分布直方图的性质的合理运用．
练习册系列答案
名师伴你成长课时同步学练测系列答案
相关题目
3．已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（a＞0，b＞0）$的一条渐近线平行于直线l：x+2y+5=0，双曲线的一个焦点在直线l上，则双曲线的方程为（ ）
| A． | $\frac{{3{x^2}}}{25}-\frac{{3{y^2}}}{100}=1$ | B． | $\frac{{3{x^2}}}{100}-\frac{{3{y^2}}}{25}=1$ | ||
| C． | $\frac{x^2}{20}-\frac{y^2}{5}=1$ | D． | $\frac{x^2}{5}-\frac{y^2}{20}=1$ |
20．执行如图所示的程序框图，若输入x为13，则输出y的值为（ ）
| A． | 10 | B． | 5 | C． | 4 | D． | 2 |
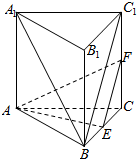如图，在三棱柱ABC-A1B1C1中，侧棱AA1⊥底面ABC，底面ABC等边三角形，E，F分别是BC，CC1的中点．求证：
4．函数f（x）=$\frac{lnx}{\sqrt{2-x}}$的定义域是（ ）
| A． | （0，2） | B． | k＞0 | C． | （0，+∞） | D． | （-∞，2） |