题目内容
17.已知f(x)=(3a-2)x+4在R上是减函数,则a的取值范围是(-∞,$\frac{2}{3}$).分析 根据一次函数单调性的性质进行求解即可.
解答 解:若f(x)=(3a-2)x+4在R上是减函数,
则3a-2<0,即a<$\frac{2}{3}$,
故答案为:(-∞,$\frac{2}{3}$)
点评 本题主要考查函数单调性的应用,根据一次函数单调性的性质是解决本题的关键.

练习册系列答案
相关题目
5.已知函数f(x)的图象是连续不断的,有如下的x,f(x)的对应表:
则函数f(x)存在零点的区间有( )
| x | 1 | 2 | 3 | 4 | 5 | 6 |
| f(x) | 136.13 | 15.552 | -3.92 | 10.88 | 12.488 | -23.064 |
| A. | 区间[2,3]和[3,4] | B. | 区间[1,2]和[4,5] | ||
| C. | 区间[2,3]、[3,4]和[4,5] | D. | 区间[2,3]、[3,4]和[5,6] |
6.在本埠投寄平信,每封信不超过20g时付邮资0.80元,超过20g而不超过40g时付邮资1.60元,依此类推,每增加20g需增加邮资0.80元(信重在100g以内),如果某人所寄的一封信的重量为82.5g,那么他应付邮资( )
| A. | 2.4元 | B. | 2.8元 | C. | 3.2元 | D. | 4元 |
7.已知f(x)是偶函数,它在[0,+∞)上是减函数,若f(ex)≥f(-e),则x的取值范围是( )
| A. | R | B. | (-∞,-1]∪[1,+∞) | C. | (-∞,1] | D. | [-1,1] |
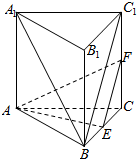 如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,底面ABC等边三角形,E,F分别是BC,CC1的中点.求证:
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,底面ABC等边三角形,E,F分别是BC,CC1的中点.求证: 已知如图几何体A1C1E1-ABCDEF底面是边长为2的正六边形,AA1,CC1,EE1长度为2且都垂直与底面.
已知如图几何体A1C1E1-ABCDEF底面是边长为2的正六边形,AA1,CC1,EE1长度为2且都垂直与底面.