题目内容
15.设a,b∈R且a<b,若a3eb=b3ea,则下列结论中一定正确的个数是( )①a+b>6;②ab<9;③a+2b>9;④a<3<b.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 令f(x)=$\frac{{x}^{3}}{{e}^{x}}$,可得f′(x)=$\frac{(3-x){x}^{2}}{{e}^{x}}$,利用导数研究函数的单调性极值与最值、图象及其性质即可得出.
解答 解:令f(x)=$\frac{{x}^{3}}{{e}^{x}}$,则f′(x)=$\frac{(3-x){x}^{2}}{{e}^{x}}$,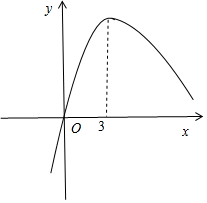
可知:x>3时,f′(x)<0,函数f(x)单调递减;
x>3时,f′(x)≥0,
函数f(x)单调递增.
x=3时,函数f(x)取得极大值即最大值.
∵f(a)=f(b),a<b.
∴0<a<3<b,a+b>6;ab<9;a+2b>9.
因此正确的答案为4个.
故选:D.
点评 本题考查了利用导数研究函数的单调性极值与最值、图象及其性质、数形结合方法,考查了推理能力与计算能力,属于难题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.已知函数f(x)=asinx+bcosx(x∈R),若x=x0是函数f(x)的一条对称轴,且tanx0=3,则点(a,b)所在的直线为( )
| A. | x-3y=0 | B. | x+3y=0 | C. | 3x-y=0 | D. | 3x+y=0 |
3.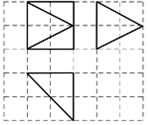 如图,网格纸上小正方形的边长为a,粗实线画出的是某多面体的三视图,此几何体的表面积为$12+4(\sqrt{2}+\sqrt{5})$,则实数a=( )
如图,网格纸上小正方形的边长为a,粗实线画出的是某多面体的三视图,此几何体的表面积为$12+4(\sqrt{2}+\sqrt{5})$,则实数a=( )
 如图,网格纸上小正方形的边长为a,粗实线画出的是某多面体的三视图,此几何体的表面积为$12+4(\sqrt{2}+\sqrt{5})$,则实数a=( )
如图,网格纸上小正方形的边长为a,粗实线画出的是某多面体的三视图,此几何体的表面积为$12+4(\sqrt{2}+\sqrt{5})$,则实数a=( )| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | 3 |
7.设P是曲线y=x-$\frac{1}{2}$x2-lnx上的一个动点,记此曲线在点P点处的切线的倾斜角为θ,则θ的取值范围是( )
| A. | ($\frac{π}{2}$,$\frac{3π}{4}$] | B. | [$\frac{π}{4}$,$\frac{3π}{4}$] | C. | [$\frac{3π}{4}$,π) | D. | [0,$\frac{π}{2}$)∪[$\frac{3π}{4}$,π) |
4.若tan($\frac{α}{2}$+$\frac{π}{4}$)=-2,则cosα的值为( )
| A. | $\frac{4}{5}$ | B. | -$\frac{4}{5}$ | C. | $\frac{3}{5}$ | D. | -$\frac{3}{5}$ |
5.某市对贫困家庭自主创业给予小额贷款补贴,每户贷款为2万元,贷款期限有6个月、12个月、18个月、24个月、36个月五种,这五种贷款期限政府分别需要补助200元、300元、300元、400元,从2016年享受此项政策的困难户中抽取了100户进行了调查,选取贷款期限的频数如表:
以上表各种贷款期限频率作为2017年贫困家庭选择各种贷款期限的概率.
(1)某小区2017年共有3户准备享受此项政策,计算其中恰有两户选择贷款期限为12个月的概率;
(2)设给享受此项政策的某困难户补贴为ξ元,写出ξ的分布列,若预计2017年全市有3.6万户享受此项政策,估计2017年该市共需要补贴多少万元.
| 贷款期限 | 6个月 | 12个月 | 18个月 | 24个月 | 36个月 |
| 频数 | 20 | 40 | 20 | 10 | 10 |
(1)某小区2017年共有3户准备享受此项政策,计算其中恰有两户选择贷款期限为12个月的概率;
(2)设给享受此项政策的某困难户补贴为ξ元,写出ξ的分布列,若预计2017年全市有3.6万户享受此项政策,估计2017年该市共需要补贴多少万元.
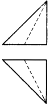
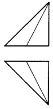
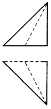
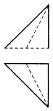
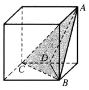 如图是一个正方体,A,B,C为三个顶点,D是棱的中点,则三棱锥A-BCD的正视图,俯视图是(注:选项中的上图是正视图,下图是俯视图)( )
如图是一个正方体,A,B,C为三个顶点,D是棱的中点,则三棱锥A-BCD的正视图,俯视图是(注:选项中的上图是正视图,下图是俯视图)( )