题目内容
7.设P是曲线y=x-$\frac{1}{2}$x2-lnx上的一个动点,记此曲线在点P点处的切线的倾斜角为θ,则θ的取值范围是( )| A. | ($\frac{π}{2}$,$\frac{3π}{4}$] | B. | [$\frac{π}{4}$,$\frac{3π}{4}$] | C. | [$\frac{3π}{4}$,π) | D. | [0,$\frac{π}{2}$)∪[$\frac{3π}{4}$,π) |
分析 求出原函数的导函数,利用基本不等式求出导函数的值域,结合直线的斜率是直线倾斜角的正切值求解.
解答 解:由y=x-$\frac{1}{2}$x2-lnx,得y′=1-x-$\frac{1}{x}$(x>0),
∵1-x-$\frac{1}{x}$=1-(x+$\frac{1}{x}$)$≤1-2\sqrt{x•\frac{1}{x}}=-1$,
当且仅当x=1时上式“=”成立.
∴y′≤-1,即曲线在点P点处的切线的斜率小于等于-1.
则tanθ≤-1,
又θ∈[0,π),
∴θ∈($\frac{π}{2},\frac{3π}{4}$].
故选:A.
点评 本题考查利用导数研究过曲线上某点处的切线方程,过曲线上某点处的切线的斜率,就是函数在该点处的导数值,是中档题.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
19.某四棱锥的三视图如图所示,则该四棱锥的侧面积为( )
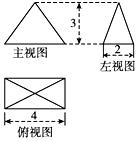

| A. | 8 | B. | 8+4$\sqrt{10}$ | C. | 4$\sqrt{10}$+2$\sqrt{13}$ | D. | 2$\sqrt{10}$+$\sqrt{13}$ |
17.在方程|x|+|y|=1表示的曲线所围成的区域内(包含边界)任取一点P(x,y),则z=xy的最大值为( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{8}$ |